- 16 июля 2025
- 9 минут
- 11 421
Умножение обыкновенных дробей: правила, примеры, решения
Статью подготовили специалисты образовательного сервиса Zaochnik.
Еще одно действие, которое можно выполнять с обыкновенными дробями, – умножение. Мы попробуем разъяснить его основные правила при решении задач, покажем, как умножается обыкновенная дробь на натуральное число и как правильно выполнить умножение трех обыкновенных дробей и больше.
Как умножить одну обыкновенную дробь на другую
Запишем сначала основное правило:
Если мы умножим одну обыкновенную дробь, то числитель дроби, полученной в результате, будет равен произведению числителей исходных дробей, а знаменатель – произведению их знаменателей. В буквенном виде для двух дробей и это можно выразить как .
Посмотрим на примере, как правильно применить это правило. Допустим, у нас есть квадрат, сторона которого равна одной числовой единице. Тогда площадь фигуры составит кв. единицу. Если разделить квадрат на равные прямоугольники со сторонами, равными и числовой единицы, у нас получится, что он теперь состоит из прямоугольников (потому что ). Соответственно, площадь каждого из них будет равна от площади всей фигуры, т.е. кв. единицы.
Далее нам надо выделить цветом часть исходного квадрата так, как это сделано на рисунке:
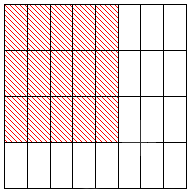
У нас получился закрашенный фрагмент со сторонами, равными числовой единицы и числовой единицы. Соответственно, для вычисления его площади надо умножить первую дробь на вторую. Она будет равна кв. единиц. Но мы можем просто подсчитать, сколько прямоугольников входит во фрагмент: их , значит, общая площадь составляет квадратных единиц.
Поскольку и , мы можем записать следующее равенство:
Оно является подтверждением сформулированного нами правила умножения обыкновенных дробей, которое выражается как . Оно действует одинаково как для правильных, так и для неправильных дробей; с помощью него можно умножить дроби и с разными, и с одинаковыми знаменателями.
Разберем решения нескольких задач на умножение обыкновенных дробей.
Умножьте на .
Решение
Для начала подсчитаем произведение числителей указанных дробей, умножив на . У нас получилось . Затем вычислим произведение знаменателей и получим: . Составим их двух чисел ответ: .
Все решение можно записать так:
Ответ: .
Если в ответе у нас получилась сократимая дробь, нужно довести вычисление до конца и выполнить ее сокращение. Если же у нас получилась неправильная дробь, из нее надо выделить целую часть.
Вычислите произведение дробей и .
Решение
Cогласно изученному выше правилу, нам надо умножить числитель на числитель, а знаменатель на знаменатель. Запись решения будет выглядеть так:
Мы получили сократимую дробь, т.е. такую, у которой есть признак делимости на .
Выполним сокращение дроби: НОД , . В итоге у нас получилась неправильная дробь, из которой мы выделим целую часть и получим смешанное число: .
Ответ: .
Для удобства вычисления мы можем сократить и исходные дроби перед выполнением действия умножения, для чего нам надо привести дробь к виду . Разложим значения переменных на простые множители и одинаковые из них сократим.
Поясним, как это выглядит, используя данные конкретной задачи.
Вычислите произведение .
Решение
Запишем вычисления, исходя из правила умножения. У нас получится:
Поскольку как и , значит,.
Далее мы можем просто сократить некоторые множители и получить следующее: 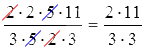 .
.
Нам осталось подсчитать несложные произведения в числителе и знаменателе и выделить целую часть из получившейся в итоге неправильной дроби:
Ответ: .
Числовое выражение, в котором имеет место умножение обыкновенных дробей, обладает переместительным свойством, то есть при необходимости мы можем изменить порядок следования множителей:
Как перемножить обыкновенную дробь с натуральным числом
Запишем сразу основное правило, а потом попробуем объяснить его на практике.
Чтобы умножить обыкновенную дробь на натуральное число, нужно умножить числитель этой дроби на это число. При этом знаменатель итоговой дроби будет равен знаменателю исходной обыкновенной дроби. Умножение некоторой дроби на натуральное число можно записать в виде формулы .
Понять эту формулу легко, если вспомнить, что любое натуральное число может быть представлено в виде обыкновенной дроби со знаменателем, равным единице, то есть:
Поясним нашу мысль конкретными примерами.
Вычислите произведение на .
Решение
В результате умножения числителя исходной дроби на второй множитель получим . В силу правила, указанного выше, мы получим в результате Все решение приведено в этой записи:
Ответ:
Когда мы перемножаем натуральное число с обыкновенной дробью, то часто приходится сокращать результат или представлять его как смешанное число.
Условие: вычислите произведение на .
Решение
По правилу выше мы умножаем натуральное число на числитель. В итоге получаем, что . Итоговая дробь имеет признаки делимости на , поэтому нам нужно выполнить ее сокращение:
НОК, значит,
Теперь нам осталось только выделить целую часть и записать готовый ответ: .
В этой записи можно видеть все решение целиком: .
Также мы могли сократить дробь с помощью разложения числителя и знаменателя на простые множители, и результат получился бы точно таким же.
Ответ: .
Числовое выражение, в котором натуральное число умножается на дробь, также обладает свойством перемещения, то есть порядок расположения множителей не влияет на результат:
Как выполнить умножение трех и более обыкновенных дробей
Мы можем распространить на действие умножения обыкновенных дробей те же свойства, которые характерны для умножения натуральных чисел. Это следует из самого определения данных понятий.
Благодаря знанию сочетательного и переместительного свойства можно перемножать три обыкновенные дроби и более. Допустимо переставлять множители местами для большего удобства или расставлять скобки так, как будет легче считать.
Покажем на примере, как это делается.
Умножьте четыре обыкновенные дроби и .
Решение: для начала сделаем запись произведения. У нас получится . Нам надо перемножить между собой все числители и все знаменатели: .
Перед тем, как начать умножение, мы можем немного облегчить себе задачу и разложить некоторые числа на простые множители для дальнейшего сокращения. Это будет проще, чем сокращать уже готовую дробь, получившуюся в результате.
Ответ: .
Перемножьте чисел .
Решение
Для удобства мы можем сгруппировать дробь с числом , а число с дробью , поскольку при этом нам будут очевидны будущие сокращения. В итоге у нас получится:
Ответ: .
Математические онлайн-калькуляторы




