- 24 июля 2025
- 8 минут
- 970
Номинальная, рыночная и текущая стоимость облигации и доход
Статью подготовили специалисты образовательного сервиса Zaochnik.
Номинальная стоимость облигации — сумма, которую берут взаймы.
Она подлежит возврату по истечении оговоренного срока, при погашении облигации. К номиналу устанавливается процент дохода. Отношение суммы всех процентных платежей, которые получают за год, к номинальной стоимости облигации именуют «купонной доходностью». А вот право получать фиксированную сумму, что обусловлено владением соответствующей облигацией, называют аннуитетом.
В основном облигации выпускают с высокой номинальной стоимостью. Именно это их отличает от акций, продажную цену которых (либо номинал) эмитент устанавливает непосредственно в расчете на их приобретение. Облигации ориентируют на индивидуальных богатых, либо на институциональных инвесторов.
На сегодняшний день в США самыми распространенными считаются облигации, номиналом в тысячу долларов. Это в тридцать раз выше, чем средняя стоимость акции на фондовой бирже в Нью-Йорке. Разумеется, нельзя сказать, что облигации недоступны людям с невысокими доходами. Ведь сумма, необходимая для покупки акции, может быть вложена косвенно, через инвестиционные фонды, которые объединяют средства мелких вкладчиков.
Рыночная стоимость и реальная доходность
Как правило, облигации являются высоколиквидным объектом инвестирования. Ведь есть и их активный вторичный рынок. Чтобы определить рыночную стоимость облигации, важно определиться с понятием конечной (будущей) и текущей стоимости.
Конечную стоимость (TV”) определяют по формуле сложных процентов:
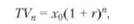
В ней I" – купонный (ссудный) процент. То есть при xо = 100 рублей и г = 8% за трехлетний период (n = 3) величина ТV будет:
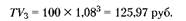
Но если проценты выплачиваются не 1 раз в год, а Т раз,
то:
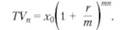
Если проценты выплачиваются поквартально, то:
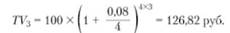
Текущая стоимость
Текущая стоимость — это стоимость денежного потока, пересчитанная на текущее время.
Она определяется по формуле:
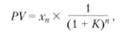
где РV — текущая стоимость денежного потока х", ее получают через n лет, а К — ставка дисконтирования.
Если х" = ТУ", то:
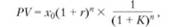
и при ставке дисконтирования, равной ссудному проценту К = г, получим РV = х$.
На рисунке показаны текущие стоимости 100 рублей, полученные через 1-10 лет при 5%, 10% и 15% ставках дисконтирования.
Чем больше процентная ставка, тем РVn меньше, и тем кривая более крутая. При ставке дисконтирования в 15% РУ 100 руб., полученные через десять лет, составляет 24,72 руб.
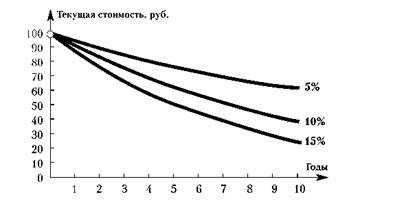
Рисунок 1. Текущая стоимость 100 руб. при ставке дисконтирования 5,10 и 15%
РV денежного потока, который представляет собой аннуитет из равновеликих выплат за определенное число временных отрезков, равна:
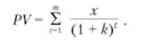
где t — число отрезков времени, за которые осуществляются выплаты х по прошествии каждого из них; £ — сумма выплат в конце отрезков времени от одного до т.
Если тысяча рублей ожидались в конце каждого из ближайших двух лет при ставке 8%:
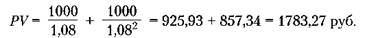
Рыночная стоимость облигации — текущая стоимость потока денежных выплат непосредственно по облигации.
Этот самый поток формируется выплатой процентного дохода за установленный период и выплатой номинальной стоимости соответствующей облигации в завершении периода.
Уравнение оценки текущей стоимости облигации при номинальной стоимостью С руб, следующее:
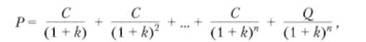
где Р — дисконтированная (текущая) стоимость потока платежей; С — процентные выплаты за год. Они определяются процентным номинальным доходом; К — норма прибыли, определяющаяся рисковостью облигации. Эта норма известна, как доход, который получают до срока погашения.
1. Необходимо определить рыночную цену облигации при номинальной стоимости 1000 рублей. Номинальный доход равен 12%. Облигация должна обеспечить до погашения установленного срока доход в 14%. Процентный номинальный доход, согласно ежегодным процентным выплатам, равен 120 рублям. Поэтому:
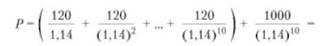
= 625,93 (стоимость потока будущих процентных выплат) + 269,74 (дисконтированная стоимость выплаты номинала) = 895,67 руб.
То есть, рыночная стоимость облигации в данном случае ниже номинальной.
2. Облигация обеспечивает в установленный период получение 10%-ного дохода.
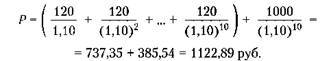
Рыночная стоимость облигации в этом случае выше номинальной. Следовательно, она изменяется в зависимости от уровня дохода.
Если необходимый уровень дохода выше установленного по облигации, стоимость облигации будет уступать номинальной стоимости. Она продается с дисконтом. Если же необходимый уровень дохода ниже установленного процентного дохода, стоимость облигации выше номинальной. То есть, продается с премией.
Если необходимый уровень дохода и установленный процентный доход равны, стоимость облигации идентична номинальной стоимости. При изменении уровня дохода показатели изменяются в зависимости от периода погашения. Из таблицы, приведенной ниже, видно, что прирост рыночной стоимости десятилетней облигации с 12% номинальным доходом равен 227,22 руб., а пятилетней — 144,48 руб. Номинальная стоимость облигации в этом случае была взята за тысячу рублей.
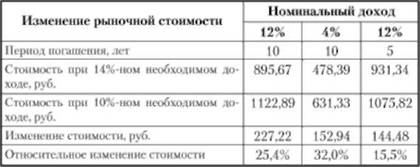
Рисунок 2. Изменение рыночной стоимости облигации при заданном изменении уровня дохода и номинальной стоимости облигации в 1000 руб.
При заданном изменении уровня дохода, стоимость облигации изменяется больше, если номинальный процентный доход ниже. При увеличении периода погашения темпы изменения рыночной стоимости будут снижаться. При номинальном доходе 12% относительное изменение стоимости облигации за 5 лет погашения — 15,5%, а за последние 5 лет — 9,9%. Чем номинальный процентный доход ниже и чем длительнее погашение облигации, тем выше степень изменчивости процентных ставок непосредственно на рынках облигации.
Определение текущей стоимости облигации
В большинстве случаев проценты облигаций выплачиваются каждые шесть месяцев. При номинале в тысячу рублей стоимость этих облигаций рассчитывается по следующей формуле:
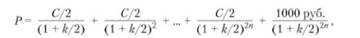
где Р — текущая рыночная цена соответствующей облигации; С — годовые выплаты процентного номинального дохода; n — число лет до погашения выпуска; & — доход, получаемый до погашения.
Уравнение стоимости содержит 4 параметра. Если задать лишь три из них, можно определить и четвертый параметр. Если Р = 960 рублей, а С= 100 рублей, при n = 12 лет, можно рассчитать необходимый доход k и уравнение запишется следующим образом:
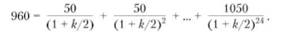
В итоге k = 10,60%. Чтобы решать такие задачи, в наше время используются специальные таблицы и калькуляторы.




