Развитие научного знания. Проблема развития научного знания

Основные аспекты проблемы научного знания

Три основные аспекта проблемы научного знания состоят в следующем:

• Ответ на вопрос, что именно составляет сущность динамики науки. А также вопросы эволюционного изменения, где расширяется объём и содержание научных истин или само развитие, как изменение со скачками, революциями, качественными отличиями во взглядах на один и тот же предмет. Подобные вопросы сопоставимы с вопросами о возможной динамике науки как кумулятивного процесса или антикумулятивного, который включает в себя отказ от прежних взглядов как неприемлемых и несоизмеримых с новыми, сменяющими их.
• Как можно интерпретировать динамику научного знания полагаясь только на его самоизменение, опираясь только на основу действий внутринаучных факторов или прилагая существенное влияние к научному знания вненаучных или социокультурных факторов?
• В чём заключаются общие закономерности развития научного знания и специфические закономерности, которые характерны для различных областей науки?

Вполне логично предположить, что ответы на данные вопросы невозможно получить, опираясь исключительно на философский анализ структурного научного сознания. Важное условие для этого видится в привлечении материала реальной истории науки. Однако, очевидно и то, что история науки не имеет возможности говорить сама за себя, и то, что она подобно любому другому внешнему опыту может обуславливаться по-разному и рационально реконструироваться. Такой тип социальной реконструкции во многом зависит от выбора, предпочтения, которое оказывается философом науки той или иной общей гносеологической позиции. Здесь имеется в виду трансцендентализм, редуционизм – антиредуционизм и т.п.

Изучение вопросов, описанных выше, занимались постпозитивисты К. Поппер, Т. Кун, И. Лакатос, Ст. Тулмин, П. Фейерабенд, М. Полани и др. Их работы в большей массе посвящены именно этой проблеме, в отличие от позитивистов, которые считали единственным "законным" предметом философии науки логический анализ структуры ставшего научного знания.

Динамика науки: кумулятивизм или антикумулятивизм

Дело в том, что ответы на вопросы о динамике научного знания нельзя дать без обращения к материалу истории науки, это происходит из-за того, что последняя была весьма справедливо объявлена постпозитивистами "пробным камнем" истинности предполагаемых моделей развития научного знания. Но при этом зачастую упускается важный аспект: предполагаемые постпозитивистами модели динамики научного знания опирались и на историю науки, и на конкретное понимание ими структуры научного знания и вытекающие из этого понимания разделение разных компонентов науки на внутренние и внешние. Таким образом, можно говорить о том, что с позиции попперовской модели динамики научного знания процесс открытия научных законов является внешним фактором для динамики науки, а в моделях М. Малкея и Дж. Гилберта является внутренним.

Абсолютное большинство постпозитивистов считали, что психологические и социальные детерминанты принадлежат к внешней истории науки. Но необходимо заметить, что Т. Кун, М. Полани и П. Фейеранбенд говорили о том, что психологические и социальные детерминанты принадлежат к внутренней истории науки. К. Поппер утверждает, что факты есть абсолютная ценность науки, они неоспоримы, общезначимы и кумулятивны. А вот Т. Кун интерпретировал факты как относительную ценность, в силу того, что они не общезначимы. Он полагал, что их объяснение находится в некоторой зависимости от принятой господствующей теории – парадигмы, именно поэтому развитие фактуального знания некумулятивно.

Рассуждая об истинной природе научного знания, важно учитывать тот факт, что пусть и все они совершаются в научном сознании, их содержание полностью зависит не только от сознания и того опыта, что был накоплен, а ещё и результатов взаимодействия сознания учёных с определённой, внешней им объектной действительностью, которую они хотят познать.

В последствие можно проследить, как убедительно показывает действительность истории науки, что все когнитивные изменения, которые в ней происходят, носят эволюционный или иными словами направленный и необратимый характер. Это свидетельствует о том, что общая риманова геометрия, к примеру, не могла зародиться раньше евклидовой, а теория относительности и квантовая механика – раньше или одновременно с классической механикой. Существует мнение, что это объясняется с позиции трактовки процесса научного познания как накопления и последующего обобщения фактов. Таким образом, весьма целесообразно говорить о том, что эволюция научного знания естественно трактуется как движение в сторону всё больших обобщений, а под сменой научных теорий подразумевается, как замена менее общей теории более общей.

Понятие "степень общности" с точки зрения науки логики объясняется обычно экстенсивно. Это значит, что понятие А имеет более общий характер, чем понятие В, в случае, когда все элементы объёма понятия В включены в объём понятия Л, обратное невозможно. Взгляд на научное познание как на обобщение фактов, на эволюцию научного знания как на увеличение степени общности сменяющихся друг друга теорий – это, естественно, индуктивистская концепция науки и её истории, которая продлилась до середины XX в. Ключевым аргументом в его защиту был принцип соответствия, который базировался на отношении между старой и новой теорией, где все положения предшествующей теории (и тем самым все факты, которые она объясняла и предсказывала) становились результатом частного случая из новой теории.

Но важно отметить, что при более строгом и глубоком анализе соотношение указанных понятий никакого частного или даже предельного случая в отношениях между ними не получается.

В качестве очередного примера необходимо рассмотреть уравнение, которое связывает значения протяжённости тела в классической и релятивистской механике:

где/-длина движущегося тела; /0 - длина покоящегося тела; V - скорость движения тела; с - скорость света.

Данное уравнение говорит о том, что с увеличением VI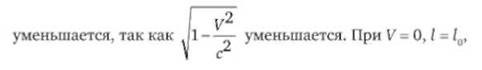 

Но это лишь один случай самой классической механики, при том её статики, но не динамики. При У=с уравнение не имеет математического смысла. А ведь только при рассмотренных значениях V возможно логическое выведение значения длины тела в классической механике из уравнений длины тела в релятивистской механике в качестве частного случая. "Частного случая" не получилось.

Таким образом, можно говорить о том, что в более высокой степени, осмысленной является объяснение классической механики в роли "предельного случая" релятивистской механики. На самом деле в случае последовательного уменьшения V значение I все больше стремится к значению /0, но никогда его не достигает (по самому смыслу релятивистской механики), поэтому /0 - не может быть рассмотрено и в качестве "предельного случая" /, так как это возможно только при исчезновении самого движения тела (при V = 0). Становится понятным, что выражение "предельный случай" не может в данном случае иметь строгое значение, а имеет скорее метафорическое.

Логично говорить о том, что длина тела меняет свою величину в процессе движения, или не меняет. Других вариантов нет. Классическая механика полностью отвергает возможность подобного изменения, релятивистская, в свою очередь, вещает о противоположном. Отсюда можно сделать вывод, что классическая и релятивистская механика противоречат друг другу с точки зрения логики. Именно об этом и говорили постпозитивисты. Они теоретически несоизмеримы друг с другом, в силу того, что у них нет общего нейтрального эмпирического базиса для сравнения. Они говорят по большей части о разных и порой даже совершенно несовместимых вещах.

Что-то подобное можно сказать и по отношению к другим примерам, которые предлагали кумулятивисты. Так, классическая механика базируется на том, что в любой момент можно одновременно задать конкретное значение двух переменных – координаты физического тела и его импульса. Квантовая механика, говорит об обратном, утверждая, что это сделать невозможно по принципу неопределённости Гейзенберга.

Когда разговор заходит о современной синтетической теории эволюции, то необходимо учитывать, что она не представляет собой механическую сумму положений аутентичной дарвиновской теории эволюции или менделеевской генетики. В силу этих обстоятельств они противоречат друг другу в понимании характера эволюции. Это обуславливается тем, что номогенез в дарвиновской теории эволюции видов посредством естественного отбора и в общем носят случайный характер эволюции в менделеевской генетике.

Такое же отрицательное заключение можно сделать и в отношении действия принципа соответствия и применительно к эволюции математического знания. Здесь речь идёт о принципе Ганкеля. Выражаясь боле точно, можно говорить о том, что арифметика действительных чисел представляет собой обобщение арифметики рациональных чисел, а последняя является обобщением арифметики натуральных чисел. Необходимо эти утверждения опровергнуть.

Все рациональные числа имеют вид -, где тип – натуральные числа. Иначе говоря, рациональные числа представляют собой суть отношения между натуральными числами, но не сами эти числа.

Очевидно, когда результат деления целое число, то особенно в случаях, когда п = 1, тогда значение функции - является одним из натуральных чисел. Строго выражаясь, натуральные числа могут быть рассмотрены как множество чисел, равномощное одному из подмножеств множества рациональных числе. Однако, это не означает, что натуральные числа представляют собой множество рациональных, ввиду того, что числа данного вида по-прежнему остаются рациональными, а не натуральными. Совсем иначе дело обстоит, когда каждому натуральному числу можно поставить в соответствие лишь одно рациональное вида -. Это означает, что множество натуральных чисел может быть "изоморфно вложено" в множество рациональных чисел. Обратное неверно. Но быть "изоморфно вложенным" не всегда значит быть "частным случаем".

Это можно утверждать и в отношении соотношения рациональных и действительных чисел.

Действительные числа по своему синтаксическому представлению – это бесконечно-местные предикаты вида Л (х, у, г, ...), тогда как рациональные – только двухместные предикаты. Логично предположить, что можно установить изоморфизм соответствия между подмножеством действительных чисел вида а1,Ь1,Ь2,Ьз,Ь4... (когда Ь1,Ь2,Ьз,Ь4... равно 0) и множеством рациональных чисел. НО важно понимать, что именно благодаря символу "…", которым обозначается бесконечность, множество действительных чисел не просто бесконечно, а несчётно бесконечно. Одновременно с тем множество рациональных чисел – счётное бесконечно. В данной ситуации принцип Ганкеля не оправдывает себя. Это обуславливается тем, что арифметика действительных чисел не представляет собой обобщение арифметики рациональных чисел, а последняя, что соответственно, не представляется "частным случаем" первой.

Соотношение евклидовой и неевклидовой геометрий

Говоря о соотношении евклидовой и неевклидовой геометрий стоит упомянуть, что последние не представляют собой обобщение первой, поскольку синтаксически многие утверждают, что эти разные геометрии противоречат друг другу.

Геометрия Лобачевского предполагает, что через точку на плоскости по отношению к данной прямой проводится более одной параллельной ей прямые линии, тогда сумма углов любого треугольника будет меньше 180°, что отношение длины любой окружности к её диаметру всегда больше я. Частная риманова геометрия: через точку на плоскости по отношению к данной прямой невозможно провести ни одной параллельной ей прямой линии, сумма углов любого треугольника всегда больше 180°, Естественно, ни о каком-либо обобщении геометрии Лобачевского и Римана по отношению к геометрии Евклида не может быть и речи, поскольку они просто противоречат последней.

Однако можно избежать противоречий между ними. В том случае, когда дополнительный параметр, как кривизна непрерывной двухмерной поверхности. В этой ситуации их можно развести по разным предметам. Утверждения геометрии Евклида верны только для поверхностей с коэффициентом кривизны 0. Положение геометрии Лобачевского исполняются на двухмерных поверхностях с постоянной отрицательной кривизной (коэффициент кривизны имеет одно из фиксированных значений в континууме {0....-1}, исключая крайние значения). Согласно положениям частной римановой геометрии, наоборот, выполняются на двухмерных поверхностях с постоянной положительной кривизной, где коэффициент кривизны имеет одно из фиксированных значений в континуальном интервале {0.... + 1}, исключая крайние значения. В конечном итоге, представляется возможным только одна евклидова геометрия и бесконечное множество геометрий Лобачевского и Римана. Чуть позднее, Риман сделал соответствующее обобщение относительно этих случаев в построенной им общей римановой геометрии, в которой кривизна пространства является не постоянной, а переменной величиной. Но это обобщение носит исключительно формальный характер, поскольку не оказывает никакого содержательного влияния на решение вопроса о соотношении евклидовой геометрии и неевклидовой.

Приходим к выводу, что геометрия Евклида не является частным случаем ни геометрии Лобачевского, ни геометрии Римана, поскольку последние "не имеют права" принимать значение коэффициента кривизны 0. Вполне возможно, что евклидова геометрия может интерпретироваться как предельный случай неевклидовых геометрий. Но это тоже нет. Поясним:

• Понятие "предельный случай" качественное и нестрогое.
• Плоскость Евклида представляет собой предел внутренней или внешней поверхности шара, но при всём при этом, можно утверждать, что евклидова прямая и есть "предельный случай" треугольника Лобачевского, а евклидова окружность "предельный случай" треугольника Римана.

Становится понятно, что подобные утверждения бессодержательны в той же степени, что и нестроги. Иначе говоря, понятие "предельного случая" должно быть скрыто за качественными отличиями между разными явлениями, потому что при желании всё может быть названо "предельным случаем" другого. Это становится возможным из-за метафоричности и нестрогости данного понятия.

Важно понимать, что в конечном итоге принцип соответствия с его опорой "предельный случай" не может быть рассмотрен как адекватный механизм рациональной реконструкции эволюции научного знания. Таким образом, основанный на нём теоретический кумулятивизм, по сути является редукционистской версией эволюции науки, которая в основной массе отрицала качественные скачки в смене фундаментальных научных теорий, и, естественно, научные революции в динамике научного знания.

Признаком того, что эволюция научного знания носит развивающийся характер, является наличие качественных скачков в динамике научного знания. Это тот случай, когда научные теории ставят под вопрос истинность старых теорий по причине того, что они не могут быть совместимы друг с другом по нескольким утверждениям о свойствах и отношениях объектов одной и той же предметной области.

В том случае, когда совершаются попытки "развести" старую и новую теории по разным предметным областям, считая каждую из них истинной в своей области, то чаще всего, пытаются перемудрить, выдавая желаемое за действительное.

В первую очередь это происходит потому, что данное высказывание не является строгим, в силу того, что не может точно определить границу, где начинается "большая масса" и "большая скорость". А во вторую – релятивистские эффекты либо имеют место при любых скоростях, либо нет. Таким образом, классическая и релятивистская механики несовместимы в своих ответах. Совсем иная ситуация, когда при малых скоростях релятивистский эффект имеет меньшее значение, чем при больших, и с практической точки зрения этот эффект может не учитываться. Но не учитывая его – не означает отрицать его существование.

Важно сделать акцент на несовместимость старой и новой научной теории, которая не является полной, а лишь частичной. Во-первых, стоит сказать о том, что многие их постулаты не только не противоречат друг другу, но и имеют полное совпадение. Во-вторых, это значит, что старая и новая теории соизмеряются частично, поскольку вводят часть понятий абсолютно одинаково.

Самый сложный выбор в науке – это выбор наиболее предпочтительной из конкурирующих теорий, как говорили классики науки, среди которых А. Эйнштейн, М. Планк, А. Пуанкаре, Н. Бор и др., это многофакторный и длительный процесс. Он не сводится только к тому, чтобы определить степень соответствия каждой из теорий имеющимися фактами, а ещё и к логико-эмпирической реконструкции процесса научного познания.  

Это отразили в своих работах Т. Кун, П. Фейерабенд, М. Малкей и др. Они смогли ярко проиллюстрировать предпочтения и смену фундаментальных научных теорий, которые учитывают не только их соответствие, но и социальных психологический и философский контекст, не только имеющимися в распоряжении учёных научные знания, но здесь ещё и вера, традиции, авторитет и даже система философских ценностей вместе философскими воззрениями, самоидентификацией исследовательских поколений и коллективов.

Т. Кун ярко передаёт переход от одной фундаментальной научной теории к другой, при этом говорит о составлении содержания научной революции, по существу или интегрально является "обращением" дисциплинарного научного сообщества в новую научную веру. Впоследствии развития научного знания этот период сменяется периодом кумулятивного, непрерывного, теоретически и эмпирически регулируемого процесса научного поиска. Это характерно для стадии нормальной науки.

Таким образом, можно говорить о том, что развитие научного знания является непрерывно-прерываемым процессом, для которого характерны время от времени качественные скачки в представлении одной и той же предметной сферы. В силу этих обстоятельств развитие научного знания представляет собой некумулятивный процесс. Невзирая на то, что наука постоянно обрастает новым объёмом эмпирической и теоретической информации, было бы довольно опрометчиво говорить о каких-либо выводах относительно прогресса в истинном содержании науки. Однозначно можно утверждать лишь о том, что старые и сменяющие их новые фундаментальные теории представляют мир кардинально иначе, чаще всего в противоположном свете. Прогрессивный взгляд на развитие теоретического знания возможен только с учётом философских догм или преформизма, или телеологизма по отношению к эволюции науки.