- 24 июля 2025
- 13 минут
- 7 595
Атом водорода. Линейчатые спектры
Статью подготовили специалисты образовательного сервиса Zaochnik.
Самым простым из всех атомов является атом водорода, и он выступил в свое время в качестве своеобразного тест-объекта для теории Бора. К моменту появления теории атом водорода был тщательно исследован в ходе экспериментов: имелось знание о том, что он содержит единственный электрон. Ядром атома является протон.
Протон - это частица с положительным зарядом, модуль которого равен модулю заряда электрона, а масса больше массы электрона в раз.
Серия Бальмера и формула Ридберга
Начало XIX века ознаменовалось открытием линейчатого спектра.
Линейчатый спектр - это дискретные спектральные линии в видимой области излучения атома водорода.
В последующем закономерности, в соответствии с которыми ведут себя длины волн (или частоты) линейчатого спектра, подробно в количественном отношении исследовал И. Бальмер (в г.)
Серия Бальмера - совокупность спектральных линий атома водорода в видимой части спектра.
Позднее подобные серии спектральных линий обнаружились в ультрафиолетовой и инфракрасной частях спектра. В г. И. Ридберг составил запись эмпирической формулы для частот спектральных линий (формула Ридберга):
.
Для серии Бальмера . Для ультрафиолетовой серии (серия Лаймана) .
Неизменяемая в формуле для частот спектральных линий носит название постоянной Ридберга и равна: .
До того, как Бор сформулировал постулаты, вопросы, каким же образом возникают линейчатые спектры и каков смысл целых чисел, входящих в формулы спектральных линий водорода (и некоторых других атомов), оставались без ответа.
Правило квантования
Постулаты Бора задали направление для развития новой науки – квантовой физики атома. Однако в них не было «рецепта», как определить параметры стационарных состояний (орбит) и соответствующих им значений энергии .
Бором было сформулировано правило квантования, которое приводило к соотносимым с опытом значениям энергий стационарных состояний атома водорода. Ученый выдвинул гипотезу, что момент импульса электрона, совершающего вращение вокруг ядра, может принимать лишь дискретные значения, кратные постоянной Планка.
Для круговых орбит правило квантования Бора имеет запись:
.
В данном выражении является массой электрона, - его скоростью, обозначает радиус стационарной круговой орбиты.
Правило квантования Бора дает возможность путем вычисления определить радиусы стационарных орбит электрона в атоме водорода и отыскать значения энергий. Скорость электрона, который совершает вращение по круговой орбите некоторого радиуса в кулоновском поле ядра, записывается в виде соотношения (в соответствии с законом Ньютона):
.
Самой близкой к ядру орбите соответствует значение .
Боровский радиус - это радиус первой орбиты, расположенной ближе всех к ядру электрона атома водорода, определяемый как:
.
Радиусы последующих орбит получают возрастание пропорционально .
Полная механическая энергия системы из атомного ядра и электрона, вращающегося по стационарной круговой орбите радиусом , имеет запись:
.
Заметим, что , поскольку имеет место действие сил притяжения между электроном и ядром. Подставим в это выражение записи для и и получаем:
.
В квантовой физике атома целое число носит название главного квантового числа.
В соответствии со вторым постулатом Бора: когда электрон переходит с одной стационарной орбиты с энергией на другую стационарную орбиту с энергией , атом испускает квант света с частотой , равной :
.
Это выражение полностью идентично с эмпирической формулой Ридберга для спектральных серий атома водорода, если за постоянную взять:
.
Подставим в это выражение числовые значения всех переменных, получим
.
Полученное значение отлично коррелируется с эмпирическим значением .
На рисунке проиллюстрировано образование спектральных серий в излучении атома водорода при переходе электрона с высоких стационарных орбит на более низкие.
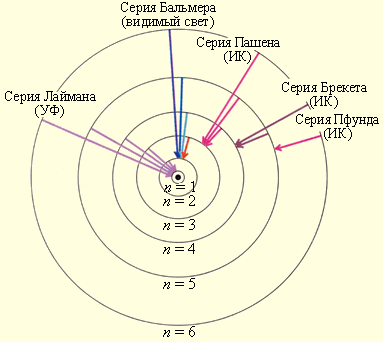
Рисунок Стационарные орбиты атома водорода и образование спектральных серий.
Рисунок демонстрирует диаграмму энергетических уровней атома водорода с указанием переходов для различных спектральных серий.
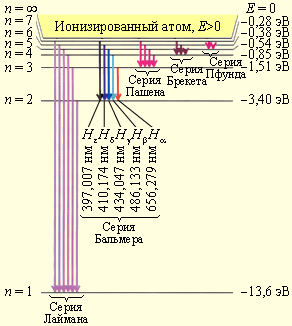
Рисунок Диаграмма энергетических уровней атома водорода с указанием переходов для различных спектральных серий. Также имеется указание длин волн для первых пяти линий серии Бальмера.
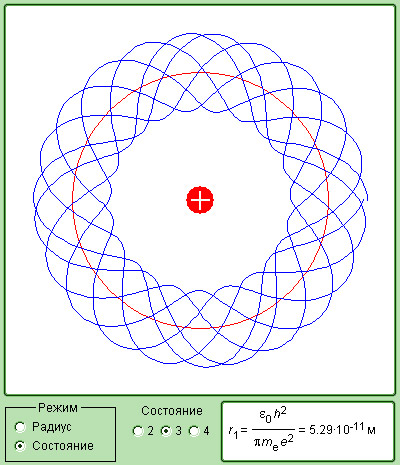
Тот факт, что теория Бора для атома водорода и результаты эксперимента оказались так отлично согласованы между собой, стал весомым аргументом в пользу верности этой теории. Но при этом попытка использовать теорию применительно к более сложным атомам закончилась провалом. Бору не удалось дать физическую интерпретацию правилу квантования – это позже, спустя десятилетие, сделал де Бройль, опираясь на представления о волновых свойствах частиц. Его предположение заключалось в том, что каждая орбита в атоме водорода соответствует волне, получающей распространение по окружности около ядра атома. Стационарная орбита имеет место тогда, когда волна постоянно повторяет себя после каждого оборота вокруг ядра. Иначе говоря, стационарная орбита соответствует круговой стоячей волне де Бройля на длине орбиты (рис. ). Такое явление подобно стационарной картине стоячих волн в струне с закрепленными концами.
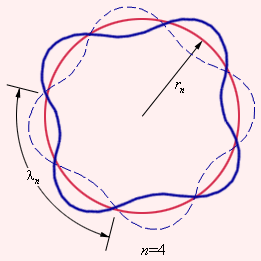
Рисунок Иллюстрация идеи де Бройля возникновения стоячих волн на стационарной орбите для случая .
Согласно дебройлевским идеям, в стационарном квантовом состоянии атома водорода на длине орбиты должно укладываться целое число длин волн :
Если подставить сюда формулу длины волны де Бройля , где – импульс электрона, то:
или .
Итак, правило квантования Бора находится во взаимосвязи с волновыми свойствами электронов.
Вообще можно сказать, что Бор достиг поразительных успехов в попытках объяснить спектральные закономерности. Появилось утверждение, что атомы являются квантовыми системами, а энергетические уровни стационарных состояний атомов дискретны. Практически одномоментно с возникновением боровской теории экспериментально было доказано, что существуют стационарные состояния атома и квантование энергии. Дискретность энергетических состояний атома опытным путем продемонстрировали в г. Д. Франк и Г. Герц, исследуя столкновение электронов с атомами ртути. Выяснилось, что при энергии электронов менее их столкновение с атомами ртути протекает согласно закону абсолютно упругого удара. А, когда энергия электронов равна , столкновение с атомами ртути будет иметь черты неупругого удара. Таким образом, выходит, что, столкнувшись с неподвижными атомами ртути, электроны лишаются всей своей кинетической энергии, что, в свою очередь, означает факт поглощения атомами ртути энергии электрона и перевода электронов из основного состояния в первое возбужденное состояние:
.
В соответствии с концепцией Бора, когда будет происходить обратный самопроизвольный переход атома, ртуть будет испускать кванты с частотой
.
Линия спектра с подобной частотой в самом деле нашлась в ультрафиолетовой части спектра излучения атомов ртути.
Утверждения о дискретных состояниях находились в противоречии с классической физикой, в связи с чем также возник закономерный вопрос: не опровергает ли квантовая теория законы классической физической теории.
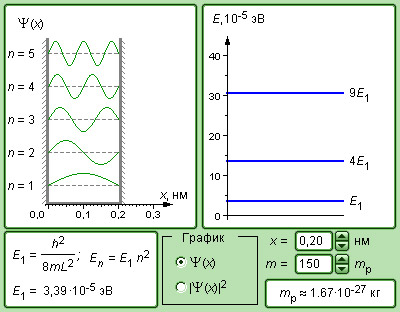
Квантовая физика отнюдь не стремилась отменить фундаментальные основы, такие как законы сохранения энергии, импульса, электрического разряда и подобное. По сформулированному Бором принципу соответствия квантовая физика вмещает в себя классические представления, и при некоторых условиях можно заметить планомерный переход от квантовых представлений к классическим. Энергетический спектр атома водорода как раз дает нам такой пример (рис. ): при больших квантовых числах дискретные уровни постепенно становятся ближе, что задает плавный переход в область непрерывного спектра, вытекающего из классической физики.
Постулаты Бора со своей «половинчатостью», «полуклассикой» стали важной ступенью развития квантовых основ, введение которых в физику потребовало серьезной перестройки механики и электродинамики, произошедшей в -е – -е годы XX века.
Квантовые числа
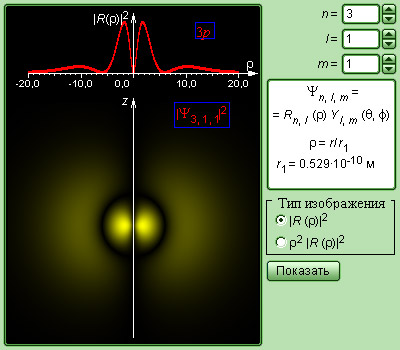
Видение Бора о том, что существуют определенные орбиты для движения электронов в атоме, оказалось очень условным. В действительности, траектория движения электрона в атоме почти не имеет общего с движением планет или спутников. Физический смысл есть лишь в возможности обнаружить электрон в том или ином месте, и эта вероятность описывается квадратом модуля волновой функции . Волновая функция служит решением базового уравнения квантовой механики – уравнения Шредингера. Выяснилось, что состояние электрона в атоме описывается целым набором квантовых чисел.
Основное квантовое число - квантовое число, задающее квантование энергии атома.
Орбитальное квантовое число – число, применяемое для квантования момента импульса.
Магнитное квантовое число – число, применяемое для квантования проекции момента импульса.
Квантовое число введено в связи с тем, что проекция момента импульса на любое выделенное в пространстве направление (к примеру, направление вектора магнитного поля) также принимает дискретный ряд значений.
Все виды квантовых чисел находятся во взаимосвязи с правилами квантования. К примеру, орбитальное квантовое число может принимать значения целого числа от до . Магнитное квантовое число может принимать любые значения целого числа в интервале . Тогда каждому значению главного квантового числа
Описываются
Когда
Рис.
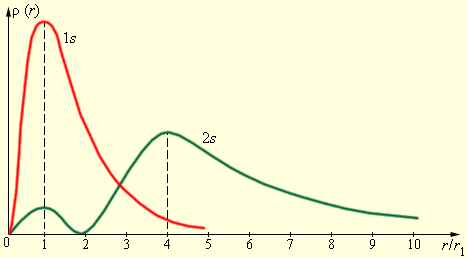
Рисунок
На рисунке
Рисунок
Рисунок
Рисунок




