- 24 июля 2025
- 6 минут
- 2 883
Эквипотенциальные поверхности
Статью подготовили специалисты образовательного сервиса Zaochnik.
Графическое изображение полей, может быть составлено как с линиями напряженности, так и при помощи разности потенциалов.
Если точки с равными потенциалами будут соединены в электрическом поле, то сформируются поверхности равного потенциала или же эквипотенциальные поверхности.
В месте пересечения с плоскостью чертежа эквипотенциальные поверхности дают эквипотенциальные линии. Изобразив соответствующие разным значениям потенциала эквипотенциальные линии, мы получаем наглядную картину, отражающую изменение потенциала конкретного поля. Перемещение вдоль эквипотенциальной поверхности заряда не требует выполнения работы, по той причине, что все точки поля на такой поверхности обладают эквивалентными потенциалами, а сила, которая воздействует на заряд, в любой момент времени ортогональна перемещению. Соответственно, линии напряженности всегда направлены под прямым углом поверхностям с одинаковыми потенциалами. Максимально наглядное изображение поля будет представлено, если отмечать эквипотенциальные линии с равными изменениями потенциала, к примеру, в и так далее. В подобном случае скорость изменения потенциала обратно пропорциональна расстоянию между соседними эквипотенциальными линиями. Что это значит?
Густота эквипотенциальных линий пропорциональна напряженности поля.
С повышением напряженности поля линии изображаются все более тесно. Обладая знанием эквипотенциальных линий, можно построить линии напряженности рассматриваемого поля и наоборот. Таким образом, изображения полей с использованием эквипотенциальных линий и линий напряженности - равноправны.
Нумерация эквипотенциальных линий на чертеже
В большей части случаев изображенные на чертеже эквипотенциальные линии нумеруют. Для того чтобы обозначить разность потенциалов на изображении, одну из линий обозначают цифрой , возле всех оставшихся линий расставляют цифры и так далее. Данные цифры в вольтах указывают разность потенциалов избранной эквипотенциальной линии и случайно выбранной нулевой линии. Стоит обратить внимание на то, что в качестве нулевой может выступать любая линия, ведь физический смысл заключается лишь в разности потенциалов двух поверхностей и зависимостью от выбранной линии не обладает.
Поле точечного заряда с положительным зарядом
В качестве примера рассмотрим поле обладающего положительным значением точечного заряда. Линиями поля точечного заряда являются радиальные прямые, соответственно, эквипотенциальные поверхности представляют собой систему концентрических сфер. Линии поля под прямым углом направлены к поверхностям сфер в любой точке поля. Роль же эквипотенциальных линий же играют концентрические окружности. Для положительного заряда рисунок представляет эквипотенциальные линии. Для отрицательного заряда рисунок представляет эквипотенциальные линии.
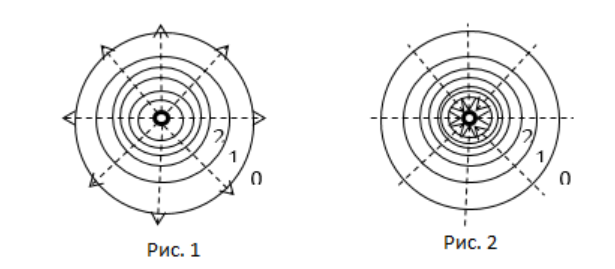
Из формулы, которая определяет потенциал поля точечного заряда при нормировке потенциала на бесконечность , очевидно, что:
.
Совокупность параллельных плоскостей, которые располагаются я на одинаковых расстояниях друг от друга, является эквипотенциальными поверхностями однородного электрического поля.
Примеры решения задач
Задание: Потенциал поля, созданный системой зарядов, имеет вид:
, где - постоянные больше нуля. Какова форма имеют эквипотенциальных поверхностей?
Решение
Эквипотенциальные поверхности, как нам известно, представляют из себя поверхности, в которых в любых точках потенциалы равны. Зная о сказанном выше, исследуем уравнение, которое приведено в условиях задачи. Разделим правую и левую части уравнения на , получим:
.
Запишем приведенное выше уравнение в каноническом виде:
Из данного выражения видно, что заданной фигурой является эллипсоид вращения. Его полуоси .
Ответ: Эквипотенциальная поверхность заданного поля - эллипсоид вращения с полуосями .
Задание: Потенциал поля, имеет вид: , где - постоянные, превышающие ноль. Что представляют собой эквипотенциальные поверхности?
Решение
Рассмотрим случай при . Приведем уравнение, заданное в условиях задачи к каноническому виду, для этого разделим обе части уравнения на , получим: .
Перепишем уравнение в следующем виде: .
Данное выражение представляет собой каноническое уравнение однополостного гиперболоида. Его полуоси равны
((действительная полуось), (действительная полуось), (мнимая полуось)).
Рассмотрим случай, когда .
Представим Приведем уравнение, заданное в условиях задачи к каноническому виду, для этого разделим обе части уравнения на минус модуль , получим: .
Перепишем уравнение в следующем виде:
.
Мы получили каноническое уравнение двуполостного гиперболоида, его полуоси:
((мнимая полуось), (мнимая полуось), (действительная полуось)).
Рассмотрим случай, когда . Тогда уравнение поля имеет вид: .
Перепишем данное уравнение в виде:
.
Мы получили каноническое уравнение прямого круглого конуса, который опирается на эллипс с полуосями .
Ответ: В качестве эквипотенциальных поверхностей для заданного уравнения потенциала мы получили: при - однополостной гиперболоид, при .




