Электрическое поле: основные понятия

Электрические заряды не воздействуют непосредственно друг на друга. Согласно современным представлениям, заряженные тела взаимодействуют посредством силового поля, которое создают вокруг себя.

Это силовое поле воздействует на заряженные тела с некоторой силой. Исследовать электрическое поле, которое окружает тело, несущее заряд, можно с помощью пробного заряда, величина которого незначительна. Особенностью электрического поля точечного заряда является тот факт, что оно не производит заметного перераспределения исследуемых зарядов.

Понятие напряженности электрического поля

Напряженность электрического поля – это силовая характеристика, которая используется для количественного определения электрического поля.

Второе значение термина – физическая величина, равная отношению силы, с которой поле действует на положительный пробный заряд, помещенный в данную точку пространства, к величине этого заряда.

Напряженность электрического поля можно задать формулой:

$\overrightarrow{E}=\frac{\overrightarrow{F}}{q}$.

Напряжение электрического поля является векторной величиной. Направление вектора $\overrightarrow{E}$ совпадает с направлением силы, которая воздействует на положительный пробный заряд в пространстве.

Напряженность электрического поля

Какое поле называют электростатическим?

Электростатическое поле – это электрическое поле, которое окружает неподвижные и не меняющиеся со временем заряды.

Очень часто в контексте темы электростатическое поле будет именоваться электрическим для краткости.

Электрическое поле может быть создано сразу несколькими заряженными телами. Такое поле также можно исследовать с помощью пробного заряда. В этом случае мы будем оценивать результирующую силу, которая будет равна геометрической сумме сил каждого из заряженных тем в отдельности.

Напряженность электрического поля, которая создается в определенной точке пространства системой зарядов, будет равна векторной сумме напряженностей электрических полей:

$\overrightarrow{E}=\overrightarrow{E_1}+\overrightarrow{E_2}+...$

Электрическое поле подчиняется принципу суперпозиции.

Согласно формуле, напряженность электростатического поля, которое создается точечным зарядом $Q$ на расстоянии $r$ от него, в соответствии с законом Кулона, будет равна по модулю:

$E=\frac{1}{4{\mathrm{\pi \epsilon }}_0}·\frac{Q}{r^2}$.

Это поле называется кулоновским.

В кулоновском поле направление вектора $\stackrel{\rightharpoonup }{E}$ зависит от знака заряда $Q$: если $Q>0$, то вектор $\stackrel{\rightharpoonup }{E}$ направлен по радиусу от заряда, если $Q<0$, то вектор $\stackrel{\rightharpoonup }{E}$ направлен к заряду.

Обратимся к иллюстрации. На рисунке для большей наглядности мы используем силовые линии электрического поля. Они проходят таким образом, чтобы направление вектора $\stackrel{\rightharpoonup }{E}$ в каждой из точек пространства совпадало с направлением касательной к силовой линии. Густота силовых линий соответствует модулю вектора напряженности поля.

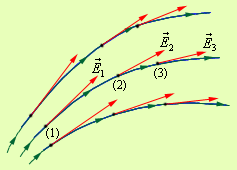
Рисунок $1.2.1.$ Силовые линии электрического поля.

Мы можем использовать как положительные, так и отрицательные точечные заряды. Оба эти случая мы изобразили на рисунке. Электростатическое поле, которое создается системой зарядов, мы можем представить как суперпозицию кулоновских полей точечных зарядов. В связи с этим мы можем рассматривать поля точечных зарядов как элементарные структурные единицы любого электрического поля.

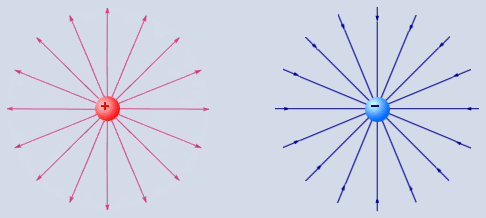
Рисунок $1.2.2.$ Силовые линии кулоновских полей.

Кулоновское поле точечного заряда $Q$ удобно записать в векторной форме. Для этого нужно провести радиус-вектор $\overrightarrow{r}$от заряда $Q$ к точке наблюдения. Тогда при $Q>0$ вектор $\overrightarrow{E}$ параллелен $\overrightarrow{r}$, а при $Q<0$ вектор $\overrightarrow{E}$ антипараллелен $\overrightarrow{r}$.

Следовательно можно записать:

$\overrightarrow{E}=\frac{1}{4\pi {\epsilon }_0}·\frac{Q}{r^3}\overrightarrow{r}$,

где $r$ – модуль радиус-вектора $\overrightarrow{r}$.

По заданному распределению зарядов можно определить электрическое поле $\overrightarrow{E}$. Такие задачи часто встречаются в таком разделе физики как электростатика. Рассмотрим пример такой задачи.

Предположим, что нам нужно найти электрическое поле длинной однородно заряженной нити на расстоянии $R$ от нее. Для большей наглядности мы привели схему на рисунке ниже.

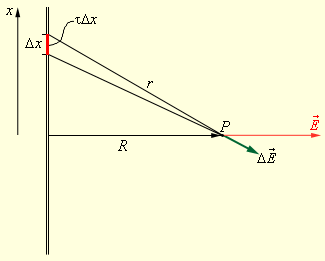
Рисунок $1.2.3.$ Электрическое поле заряженной нити.

Поле в точке наблюдения $P$ может быть представлено в виде суперпозиции кулоновских полей, создаваемых малыми элементами $\Delta x$ нити, с зарядом $\tau \Delta x$, где $\tau$ – заряд нити на единицу длины. Задача сводится к суммированию (интегрированию) элементарных полей $∆\overrightarrow{E}$. Результирующее поле оказывается равным

$E=\frac{\tau }{2\pi {\epsilon }_{0}R}$.

Вектор $\overrightarrow{E}$ везде направлен по радиусу $\overrightarrow{R}$. Это следует из симметрии задачи.

Даже в таком простом примере вычисления могут быть достаточно громоздкими. Упростить математические расчеты позволяет теорема Гаусса, которая выражает фундаментальное свойство электрического поля.

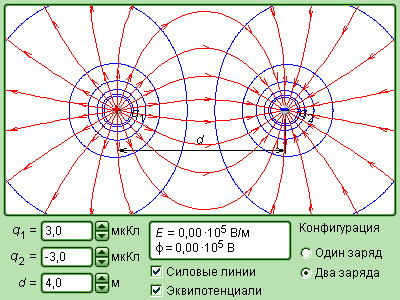
Рисунок $1.2.4.$ Модель электрического поля точечных зарядов.

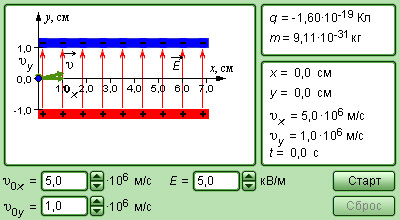
Рисунок $1.2.5.$ Модель движения заряда в электрическом поле.

Понятие о диполях

Электрический диполь – это система из двух одинаковых по модулю зарядов, которые отличаются знаками и расположены на некотором расстоянии друг от друга.

Эта система может послужить нам хорошим примером применения принципа суперпозиции полей, а также электрической моделью многих молекул.

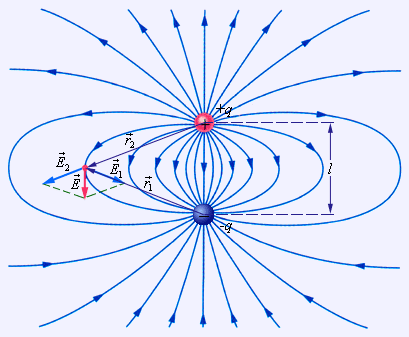
Рисунок $1.2.6.$ Силовые линии поля электрического диполя $\overrightarrow{E}=\overrightarrow{E_1}+\overrightarrow{E_2}$.

Дипольный момент $\overrightarrow{p}$ является одной из наиболее важных характеристик электрического диполя:

$\overrightarrow{p}=\overrightarrow{l}q$,

где $\overrightarrow{l}$ – вектор, направленный от отрицательного заряда к положительному, модуль $\left.open\overrightarrow{l}\right|=l$.

Электрическим дипольным моментом обладает, например, нейтральная молекула воды $\left(H_{2}O\right)$, так как центры двух атомов водорода располагаются не на одной прямой с центром атома кислорода, а под углом $105°$. Дипольный момент молекулы воды $p=6,2·{10}^{–30} Кл · м$.

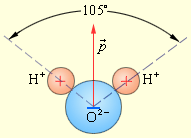
Рисунок $1.2.7.$ Дипольный момент молекулы воды.