- 24 июля 2025
- 7 минут
- 2 092
Проводники в электростатическом поле
Статью подготовили специалисты образовательного сервиса Zaochnik.
При внесении проводника в электрическое поле положительные заряды (ядра) и отрицательные (электроны) разделяются. Это явление получило название электростатической индукции. Появляющиеся заряды в результате этого процесса – индуцированные. Они создают дополнительное электрическое поле.
Направление поля таких зарядов – противоположная сторона относительно внешнего. Заряды, которые накапливаются на концах проводника, способны ослаблять внешнее поле. Их перераспределение идет до тех пор, пока не выполняются условия равновесия зарядов для проводников.
Условия равновесного состояния заряда в проводнике
Чтобы заряд на проводнике был в состоянии равновесия, необходимо:
- напряженность поля внутри равнялась нулю , то есть с неизменным потенциалом внутри поля с эквипотенциальным объемом проводника;
- направление вектора на поверхности проводника перпендикулярно относительно самого проводника в любой точке поля, при равновесном состоянии поверхности заряда наличие эквипотенциальной поверхности проводника.
Если имеется проводник, заряженный до заряда , то его распределение выполнится таким образом, что он будет находиться в равновесии. Произведем выделение замкнутой поверхности в переделах указанного тела. Внутри проводник отсутствует, поэтому поток вектора напряженности через избранную поверхность будет равняться нулю. По теореме Гаусса-Остроградского внутри поверхности зарядов нет, соответственно их сумма равна .
Выбранная поверхность – произвольная, поэтому в равновесном состоянии зарядов просто не может быть внутри. Они все распределяются по поверхности с плотностью . В проводнике отсутствуют некомпенсированные заряды, поэтому при удалении вещества из него не произойдет перемен в равновесии зарядов. Они просто не могут находиться на поверхности полости проводника в таком состоянии.
Истечение заряда с острия
При наличии большего расстояния от проводника, чем его размеры, рисунок линий похож на поле точечного заряда. Эквипотенциальные поверхности имеют форму сферы, как и у точечного заряда. Вблизи выступов эквипотенциальные поверхности располагаются гуще, тогда напряженность поля больше. Отсюда следует, что особенно большая плотность заряда наблюдается на выступах. Напряженность поля на острие может быть настолько велика, что возникает ионизация молекул газа, который окружает проводник.
Ионы газа с противоположным знаком заряда (относительно заряда проводника) притягиваются к проводнику, нейтрализуя его заряд. Ионы с одинаковыми знаками отталкиваются от проводника, причем «тянут» за собой нейтральные молекулы газа. Явление получило название электрического ветра.
Уменьшение заряда проводника происходит в процессе нейтрализации, то есть стекание с острия. Это явление называется стечением заряда с острия.
Электрическое смещение поля в однородном изотропном диэлектрике около заряженного проводника равняется:
с , обозначающей поверхность распределения зарядов и зависящей от кривизны поверхности.
Запись формулы напряженности приобретает вид:
, где - электрическая постоянная, а - диэлектрическая проницаемость среды.
На элемент поверхности проводника с площадью действует сила , которая вычисляется по формуле:
, где является напряженностью поля в диэлектрике, в точке нахождения проводника, а направлена в сторону внешней нормали к поверхности проводника.
Примеры решения задач
Описать поведение линий поля при внесении проводника, не обладающего зарядом в электростатическом поле.
Решение
Если внести нейтральный проводник в электрическое поле, то заряды разделяются на отрицательные и положительные – происходит образование индуцированных зарядов. Их перераспределение начинается с момента выполнения условий о равенстве нулю напряженности внутри проводника и перпендикулярности вектора напряженности поля поверхности проводника.
Нейтральный проводник участвует в разрыве части линий напряженности поля, они заканчиваются на отрицательных индуцированных зарядах, которые возникли на поверхности проводника, и снова начинаются с положительных. Распределение индуцированных зарядов идет по поверхности проводника, как указано на рисунке . При имеющейся полости внутри проводника в равновесном состоянии поле внутри нее равняется нулю.
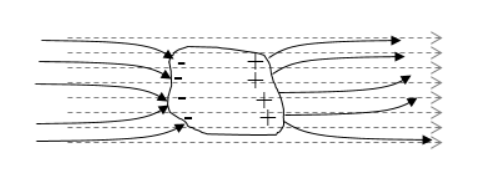
Рисунок
Положительный точечный заряд создает электростатическое поле. В него вносится шар, являющийся проводником. Какими будут эквипотенциальные поверхности и силовые линии результирующего поля?
Решение
При внесении в поле незаряженного проводящего шара, на нем индуцируются заряды, которые распределяются по поверхности шара так, чтобы внутри него поле равнялось нулю, а линии напряженности перпендикулярны к любой точке шара. На рисунке изображены распределения индуцированных зарядов.
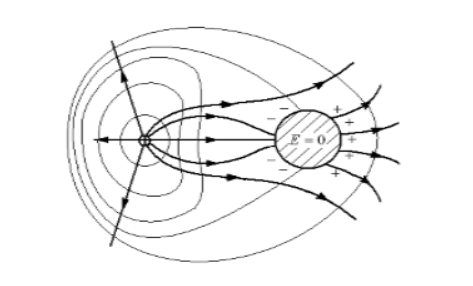
Рисунок
Если силовые линии удалять от заданной системы, то по виду они приближаются к радиальным. Эквипотенциальные поверхности результирующего поля становятся сферами.
Получить формулу напряженности поля в вакууме около поверхности заряженного проводника, если положительный заряд распределен по поверхности проводника с поверхностной плотностью .
Решение
Решение данного задания возможно при применении теоремы Гаусса-Остроградского. Необходимо выделить небольшую цилиндрическую поверхность на поверхности проводника таким образом, чтобы ось цилиндра была перпендикулярна поверхности, как показано на рисунке .
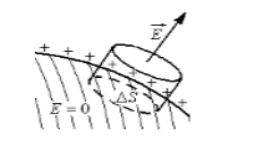
Рисунок
Расположение линий напряженности поля относительно поверхности проводника перпендикулярно и параллельно относительно осей цилиндра. Определение потока вектора напряженности через площадку , используя теорему Гаусса-Остроградского, равняется:
.
Для определения находящегося внутри выделенной поверхности заряда следует использовать формулу:
.
Далее нужно совершить подстановку в и выразить напряженность поля:
.
Ответ: . При положительном заряде направление вектора напряженности следует от поверхности.




