- 24 июля 2025
- 6 минут
- 3 770
Свободные и связанные заряды
Статью подготовили специалисты образовательного сервиса Zaochnik.
Когда рассматриваются диэлектрики в электростатических полях, следует различать два вида электрических зарядов: свободные и связанные.
Свободные заряды – это заряды, перемещающиеся под действием поля на существенные расстояния.
Например, электроны в проводниках, ионы в газах и заряды, привносимые извне на поверхность диэлектриков, которые нарушают их (диэлектриков) нейтральность. Заряды, входящие в состав нейтральных, в целом, молекул диэлектриков, так же, как ионы, закрепленные в кристаллических решетках твердых диэлектриков около положений равновесия, получили название связанных зарядов.
Поверхностная плотность зарядов
Формула потенциала электростатического поля в диэлектрике запишется как:
с , являющимся потенциалом поля, создаваемого свободными зарядами, с
- потенциалом поля, создаваемого связанными зарядами.
Известно:
, - это объемная плотность свободных зарядов, - их поверхностная плотность. Определение потенциала поля связанных зарядов:
, где служит вектором поляризации.
Можно сделать вывод, что из и получим:
.
При использовании теоремы Остроградского-Гаусса с некоторыми формулами векторного анализа имеем совсем иной вид уравнения :
,
где обозначается в качестве средней объемной плотности связанных зарядов, а - средняя поверхностная плоскость связанных зарядов. По уравнению видно, что при наличии диэлектрика электрическое поле совпадает с полем, созданным свободными зарядами плюс поле, которое создается связанными зарядами.
Плотность связанных зарядов
Если , то средняя плотность связанных зарядов равняется нулю. Это говорит о том, что накопление зарядов одного знака в диэлектрике не происходит. На границе между поляризованным диэлектриком и вакуумом или металлом сосредоточен поверхностный связанный заряд плотности:
с , являющейся нормальной компонентой вектора поляризованности диэлектрика на его границе с вакуумом.
Функция вида будет решением уравнения:
.
При и получим:
.
.
Выражение называют основным дифференциальным уравнением электростатического поля в любой произвольной среде.
Для получения полной системы уравнений электростатики, нужно использовать формулу с определением, связывающим векторы напряженности электрического поля с векторами поляризации.
Зависимость представится как:
, где служат для нумерации компонентов по осям декартовой системы координат - это тензор диэлектрической восприимчивости.
Если имеется внешнее электрическое поле, вещество становится источником поля, значит, поле изменяется.
Дан плоский конденсатор с пространством, между обкладками которого заполнено однородным изотропным диэлектриком с диэлектрической восприимчивостью . На них располагается поверхностный заряд с плотностью . Определить напряженность результирующего поля в конденсаторе.
Решение
Если при имеющихся обкладках конденсатора находится вакуум, то напряженность поля, создаваемого заряженными обкладками, запишется как:
с , являющейся электрической постоянной.
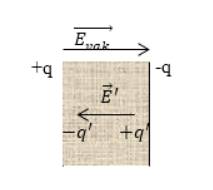
Рисунок
- это заряды, находящиеся на обкладках конденсатора.
- напряженность поля, создаваемого обкладками конденсатора.
- заряды диэлектрика.
- напряженность поля, создаваемого в результате поляризации диэлектрика.
Очевидно, что диэлектрик поляризуется, тогда напряженность уменьшается. Диэлектрик однородный, а поле, создаваемое в плоском конденсаторе, также считается однородным. Отсюда вывод – поляризованность диэлектрика однородна, иначе говоря, отсутствуют объемные связанные заряды . Имеются только поверхностные с плотностью :
.
Так как известна связь напряженности поля и вектора поляризации для изотропного диэлектрика, то
.
Отсюда получаем:
с , являющейся проекцией напряженности на внешнюю нормаль к поверхности диэлектрика.
Направление напряженности идет от стороны положительно заряженной пластины к отрицательной. Из получаем, что поверхностная плотность связанного заряда на границе с положительно заряженной пластиной отрицательная, а на границе с отрицательной пластиной – положительная. Следовательно, напряженность поля в диэлектрике между этими пластинами равняется напряженности поля в вакууме между ними, но со значением поверхностной плотности заряда, вычисляемой по формуле .
На основании выше сказанного зафиксируем, что напряженность поля в конденсаторе с диэлектриком запишется как:
.
Произведем выражение из искомой напряженности:
.
Ответ: .




