- 24 июля 2025
- 10 минут
- 16 994
Теорема Гаусса
Статью подготовили специалисты образовательного сервиса Zaochnik.
Для полноценного описания электростатического поля заданной системы зарядов в вакууме достаточно экспериментально подтвержденного закона Кулона и принципа суперпозиции. Но при этом существует возможность свойства электростатического поля охарактеризовать в ином обобщенном виде, не опираясь на утверждения касательно кулоновского поля точечного заряда.
Поток вектора напряженности
Зададим новую физическую величину, описывающую электрическое поле – поток вектора напряженности электрического поля. Предположим, что в пространстве, содержащем заданное электрическое поле, имеется некая достаточно малая площадка .
Элементарный поток вектора напряженности (через площадку ) – это физическая величина, равная произведению модуля вектора , площади и косинуса угла между вектором и нормалью к площадке:
В данной формуле является модулем нормальной составляющей поля .
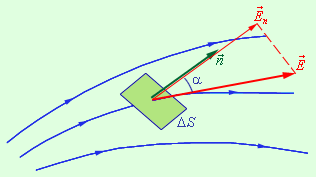
Рисунок Иллюстрация элементарного потока .
Теперь возьмем для рассмотрения некую произвольную замкнутую поверхность . Разобьем заданную поверхность на площадки небольшого размера , рассчитаем элементарные потоки поля через эти малые площадки, после чего найдем их сумму, что в итоге даст нам поток вектора через замкнутую поверхность (рис. ):
Когда речь идет о поверхности замкнутого типа, всегда используется внешняя нормаль.
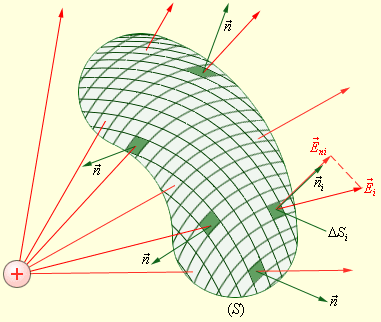
Рисунок Расчет потока через произвольную замкнутую поверхность .
Теорема Гаусса. Доказательство
Теорема или закон Гаусса для электростатического поля в вакууме является одним из основных электродинамических законов.
Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную .
Уравнение Гаусса имеет вид:
Докажем указанную теорию: для этого исследуем сферическую поверхность (или поверхность шара) . В центре заданной поверхности расположен точечный заряд . Любая точка сферы обладает электрическим полем, перпендикулярным поверхности сферы и равным по модулю:
,
где является радиусом сферы.
Поток через поверхность шара запишется, как произведение и площади сферы . Тогда: .
Следующим нашим шагом будет окружение точечного заряда произвольной поверхностью замкнутого типа; зададим также вспомогательную сферу (рис. ).
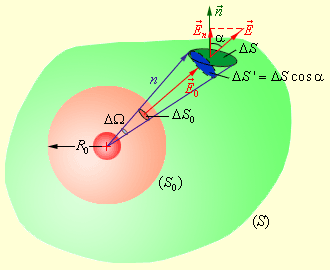
Рисунок Поток электрического поля точечного заряда через произвольную поверхность , окружающую заряд.
Возьмем для рассмотрения конус с малым телесным углом при вершине. Рассматриваемый конус задаст на сфере малую площадку , а на поверхности – площадку . Элементарные потоки и через эти площадки являются одинаковыми. В самом деле:
,
где выражением определяется площадка, которая задастся конусом с телесным углом на поверхности сферы радиуса .
Поскольку , то . Из полученного следует вывод о том, что полный поток электрического поля точечного заряда через произвольную поверхность, охватывающую заряд, равен потоку через поверхность вспомогательной сферы:
.
Так же мы можем продемонстрировать, что, когда замкнутая поверхность не охватывает точечный заряд , поток равен нулю. Этот случай проиллюстрирован на рис. . Все силовые линии электрического поля точечного заряда пронизывают замкнутую поверхность насквозь. Внутри поверхности зарядов нет, т.е. в этой области не наблюдается обрыва или зарождения силовых линий.
Обобщение теоремы Гаусса на случай произвольного распределения зарядов является следствием из принципа суперпозиции. Поле любого распределения зарядов возможно записать в виде векторной суммы электрических полей точечных зарядов. Поток системы зарядов через произвольную замкнутую поверхность сложится из потоков электрических полей отдельных зарядов. Когда заряд расположен внутри поверхности , он дает вклад в поток, равный . В случае расположения заряда снаружи поверхности его вклад в поток есть нуль.
Так, мы доказали теорему Гаусса.
Теорема Гаусса, по сути, есть следствие закона Кулона и принципа суперпозиции. Однако, взяв за изначальную аксиому утверждения теоремы, следствием станет закон Кулона, в связи с чем теорему Гаусса порой называют альтернативной формулировкой закона Кулона.
Опираясь на теорему Гаусса, в определенных случаях легко определить напряженность электрического поля вокруг заряженного тела (при наличии заранее угаданных симметрии заданного распределения зарядов и общей структуры поля).
Применение теоремы Гаусса
В качестве примера можно рассмотреть задачу, в которой необходимо вычислить поле тонкостенного полого однородно заряженного длинного цилиндра с радиусом . Такая задача имеет осевую симметрию, и из соображений симметрии электрическое поле должно иметь направление по радиусу. Таким образом, чтобы иметь возможность применить теорему Гаусса, оптимально выбрать поверхность замкнутого типа в виде соосного цилиндра некоторого радиуса и длины , закрытого с обоих торцов (рис. ).
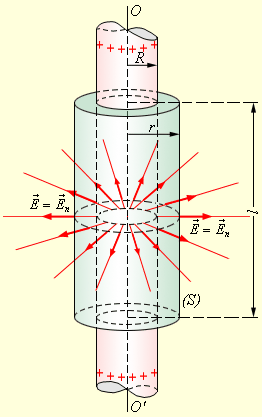
Рисунок Иллюстрация поля однородно заряженного цилиндра. – ось симметрии.
Если , то весь поток вектора напряженности пройдет через боковую поверхность цилиндра, поскольку поток через оба основания есть нуль. Формула площади боковой поверхности цилиндра запишется как: . Применим закон Гаусса и получим:
.
В указанном выражении является зарядом длины цилиндра. Далее можно записать:
.
Данное выражение не имеет зависимости от радиуса заряженного цилиндра, а значит оно применимо и к полю длинной однородно заряженной нити.
Чтобы найти напряженность поля внутри заряженного цилиндра, необходимо создать замкнутую поверхность для случая . В соответствии с симметрией задачи поток вектора напряженности через боковую поверхность цилиндра должен быть, и в этом случае он равен . Исходя из гауссовской теоремы, этот поток находится в пропорции к заряду, расположенному внутри замкнутой поверхности. Заряд этот равен нулю, откуда вытекает, что электрическое поле внутри однородно заряженного длинного полого цилиндра тоже есть нуль.
Точно так же теорема и формула Гаусса применимы для определения электрического поля в иных случаях, когда распределение зарядов охарактеризовано какой-либо симметрией, к примеру, симметрией относительно центра, плоскости или оси. Во всех этих случаях необходимо выбирать замкнутую гауссову поверхность подходящей формы.
К примеру, в случае центральной симметрии поверхность оптимально выбрать в виде сферы, у которой центр расположен в точке симметрии. Когда мы имеем симметрию относительно оси, подходящим видом замкнутой поверхности будет соосный цилиндр, закрытый с обоих торцов (аналогично рассмотренному выше примеру).
При отсутствии симметрии и невозможности угадать общую структуру поля, теорема Гаусса не сможет быть применена для упрощения решения задачи по определению напряженности поля.
Разберем еще пример распределения зарядов при наличии симметрии: нахождение поля равномерно заряженной плоскости (рис. ).
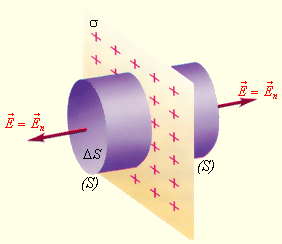
Рисунок Поле равномерно заряженной плоскости. – поверхностная плотность заряда. – замкнутая гауссова поверхность.
Здесь гауссову поверхность оптимально задать как цилиндр некой длины, замкнутый с обоих концов. Ось цилиндра является перпендикуляром к заряженной плоскости; в свою очередь, торцы цилиндра находятся на одинаковом расстоянии от нее. В соответствии с симметрией поле равномерно заряженной плоскости должно везде иметь направление по нормали. Применим теорему Гаусса и получим:
или .
Здесь является поверхностной плотностью заряда или зарядом, приходящимся на единицу площади.
Выражение, которое мы получили для электрического поля однородно заряженной плоскости, возможно использовать и для плоских заряженных площадок конечного размера: здесь расстояние от точки, в которой мы определяем напряженность поля, до заряженной площадки должно быть значимо меньше размеров площадки.




