- 24 июля 2025
- 6 минут
- 4 587
Теорема Гаусса в присутствии диэлектриков
Статью подготовили специалисты образовательного сервиса Zaochnik.
Влияние диэлектриков на электрическое поле сводится к ответному действию возникающих в поле поляризационных зарядов. Теорема Остроградского-Гауса для тел в вакууме электростатического поля может быть трансформирована с помощью добавления к свободным зарядам поляризационных для получения теоремы с диэлектриками. В этом случае она запишется как:
Со значением в качестве связанных зарядов, - свободных зарядов, - потока вектора напряженности электрического поля.
Теорема Остроградского-Гаусса
Если использовать вектор электрического смещения , то это заметно облегчает анализ поля при наличии диэлектрика. Теорему Остроградского-Гаусса при наличии диэлектрика можно записать в интегральном виде:
, где является суммарным свободным зарядом, находящийся внутри объема, который ограничен поверхностью .
Поток вектора через замкнутую поверхность может быть определен только с помощью свободных зарядов. В вакууме векторы и совпадающие.
Дифференциальная форма теоремы Гаусса выражения изображается как:
с , являющейся объемной плотностью свободных зарядов.
Теорема Остроградского-Гаусса вида и справедлива только в электростатике и выполняется для переменных полей. Ее относят к составной части системы уравнений Максвелла.
Теорема Остроградского-Гаусса в дифференциальной форме
Напомним формулу вектора электрической индукции:
со значением в качестве электрической постоянной, - вектора напряженности, - вектора поляризации.
Произведем подстановку формулы в :
.
При использовании теоремы Остроградского-Гаусса дифференциального вида, получим:
.
Для вектора напряженности вышеуказанная формула примет вид в присутствии диэлектрика:
с , являющейся плотностью заряда. В этом случае необходимо применить и :
.
Теорема Остроградского-Гаусса для диэлектриков
Теорема Остроградского-Гаусса для вектора электрического смещения в диэлектрике выглядит также, как и для напряженности поля в вакууме. Отсюда следует, что математические соотношения, получившиеся для поля в вакууме, аналогичны записям для однородного диэлектрика при замене напряженности электрического поля на вектор .
Дан диэлектрический шар, имеющий диэлектрическую проницаемость , равномерно заряжен по объему с постоянной плотностью заряда . Его нахождение в среде обусловлено наличием диэлектрической проницаемости . Изобразить график напряженности поля шара от расстояния до его центра.
Решение
Поле, создаваемое шаром по заданным условиям, имеет сферическую симметрию. Необходимо рассмотреть его внутри шара . Для нахождения выбирается сферическая поверхность с радиусом меньше сферы. По теореме Остроградского-Гаусса:
, где - площадь поверхности сферы, которая была выделена. Отсюда следует:
.
Заряд, находящийся внутри сферы, ищем из формулы:
.
Очевидно, что будут происходить изменения напряженности поля внутри шара , согласно выражениям:
,
.
Перейдем к рассмотрению поля вне шара . Для нахождения выбираем сферическую поверхность с радиусом больше радиуса сферы. По теореме Остроградского-Гаусса получим:
, где обозначает площадь поверхности выделенной сферы. Отсюда следует:
.
Формула имеет . Поэтому находящийся внутри заряд выделенной сферы находится из:
.
Далее следует подставить площадь из , заряд из , подставив в :
.
.
В результате запишем:
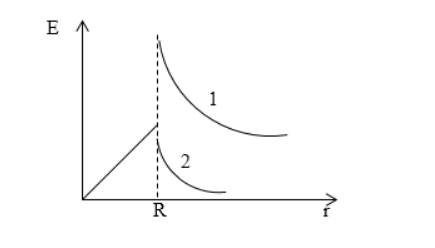
Рисунок
Ответ: графики показаны на рисунке . Внутри шара напряженность увеличивается прямо пропорционально расстоянию от центра шара. Вне шара она равняется . На границе диэлектриков происходит разрыв. Кривая под номером соответствует условию .
Предположим, что имеется воображаемая сфера, в центре которой находится точечный заряд. Будет ли изменяться поток вектора напряженности через эту поверхность, если: все пространство будет заполнено однородным и изотопным диэлектриком, произвести замену сферической поверхности на кубическую?
Решение
- По теореме Остроградского-Гаусса поток вектора напряженности через поверхность сферы в пространстве с диэлектриком будет равняться:
, со значением в качестве связанных зарядов, которые вызваны поляризацией диэлектрика полем одиночного заряда, в качестве свободного заряда, находящегося в центре сферы.
Учитывая теорему Остроградского-Гаусса, формула потока вектора напряженности через поверхность сферы в пространстве без диэлектрика примет вид:
.
- Поле было создано при помощи точечного свободного заряда, то при замене формы поверхности потока вектор напряженности не будет изменяться, потому как равняется аналогичным значению заряда, находящегося на поверхности.
Ответ:
- изменится,
- не изменится.




