- 24 июля 2025
- 6 минут
- 2 436
Уравнение Пуассона и математическая постановка задач электростатики
Статью подготовили специалисты образовательного сервиса Zaochnik.
Существует большое количество случаев, когда самым удобным методом нахождения напряженности поля считается решение дифференциального уравнения для потенциала. После его получения применим в качестве основы теорему Остроградского-Гаусса в дифференциальной форме:
где является плотностью распределения заряда, - электрической постоянной, - дивергенцией вектора напряженности и выражением, связывающим напряженность поля и потенциал.
Произведем подстановку в :
Учитывая, что , где - это оператор Лапласа, равенство принимает вид:
Выражение получило название уравнения Пуассона для вакуума. При отсутствующих зарядах запишется как уравнение Лапласа:
После нахождения потенциала переходим к вычислению напряженности, используя . Решения уравнения Пуассона должны удовлетворять требованиям:
- значение потенциала как непрерывная функция;
- потенциал должен быть конечной функцией;
- производные потенциала как функции по координатам должны быть конечными.
При наличии сосредоточенных зарядов в объеме , решение уравнения будет выражаться для потенциала вида:
Общая задача электростатики сводится к нахождению решения дифференциального уравнения, то есть уравнения Пуассона, удовлетворяющего вышеперечисленным требованиям. Теоретические вычисления известны для небольшого количества частных случаев. Если возможно подобрать функцию , удовлетворяющую условиям, то она является единственным решением.
В таких задачах не всегда необходимо задавать заряды или потенциалы во всем пространстве. Для нахождения электрического поля в полости, окруженной проводящей оболочкой, достаточно вычислить поле тел, находящихся внутри нее.
Любое решение уравнения Пуассона ограниченной области может быть определено краевыми условиями, накладывающимися на поведение решения. Границы перехода из одной среды в другую имеют условия, которые должны быть выполнены:
, или .
.
,
где - это поверхностная полость свободных зарядов, – единичный вектор нормали к границе раздела, проведенный из среды в , - единичный вектор, касательный к границе.
Эти уравнения выражают скачок нормальных составляющих вектора напряженности и непрерывность касательной вектора напряженностей электрического поля при переходе через любую заряженную поверхность независимо от ее формы и наличия или отсутствия зарядов вне ее.
Уравнение Пуассона в сферических, полярных и цилиндрических координатах
Запись уравнения может быть как при помощи декартовых координат, также и сферических, цилиндрических, полярных.
При наличии сферических уравнение Пуассона запишется как:
.
В полярных :
.
В цилиндрических :
.
Примеры решения задач
Найти поле между коаксиальными цилиндрами с радиусами и и с имеющейся разностью потенциалов .
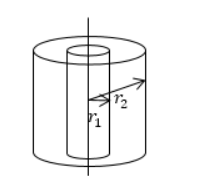
Рисунок
Решение
Необходимо зафиксировать уравнение Лапласа с цилиндрическими координатами, учитывая аксиальную симметрию:
.
Решение имеет вид . Для этого следует выбрать нулевой потенциал на нужном цилиндре, тогда:
, следовательно
.
, получим:
.
После преобразования:
.
Ответ: поле с двумя коаксиальными цилиндрами может быть задано при помощи функции .
Найти потенциал поля, которое создает бесконечно круглый цилиндр с радиусом и объемной плотностью заряда . Использовать уравнение Пуассона.
Решение
Необходимо направить ось по оси цилиндра. Видно, что цилиндрическое распределение заряда аксиально симметрично, потенциал имеет такую же симметрию, иначе говоря, считается функцией с , являющимся расстоянием от оси цилиндра. Для решения используется цилиндрическая система координат. Уравнение Пуассона в ней запишется как:
.
- это постоянные интегрирования. Имеем, что потенциал во всех точках должен быть конечным, а . Отсюда следует, что . Далее необходимо пронормировать потенциал, задействовав условие . Получим .
Поверхностные заряды отсутствуют, поэтому напряженность электрического поля на поверхности шара является непрерывной. Следовательно, что и производная от потенциала также непрерывна при , как и сам потенциал. Исходя из условий, можно найти :
.
.
Значит, полученные выражения записываются как:
Ответ: потенциал поля равняется:




