- 24 июля 2025
- 4 минуты
- 21 687
Мгновенная и средняя скорость
Статью подготовили специалисты образовательного сервиса Zaochnik.
Если материальная точка находится в движении, то ее координаты подвергаются изменениям. Этот процесс может происходить быстро или медленно.
Величина, которая характеризует быстроту изменения положения координаты, называется скоростью.
Средняя скорость – это векторная величина, численно равная перемещению в единицу времени, и сонаправленная с вектором перемещения .
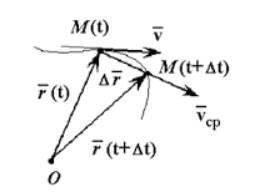
Рисунок . Средняя скорость сонаправлена перемещению
Модуль средней скорости по пути равняется .
Мгновенная скорость точки. Формулы
Мгновенная скорость характеризует движение в определенный момент времени. Выражение «скорость тела в данный момент времени» считается не корректным, но применимым при математических расчетах.
Мгновенной скоростью называют предел, к которому стремится средняя скорость при стремлении промежутка времени к :
.
Направление вектора идет по касательной к криволинейной траектории, потому как бесконечно малое перемещение совпадает с бесконечно малым элементом траектории .
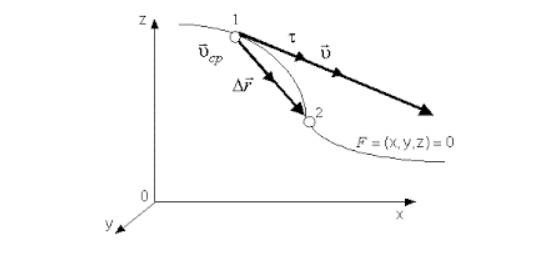
Рисунок . Вектор мгновенной скорости
Имеющееся выражение в декартовых координатах идентично ниже предложенным уравнениям:
.
Перемещение и мгновенная скорость
Запись модуля вектора примет вид:
.
Чтобы перейти от декартовых прямоугольных координат к криволинейным, применяют правила дифференцирования сложных функций. Если радиус-вектор является функцией криволинейных координат , тогда значение скорости запишется как:
.
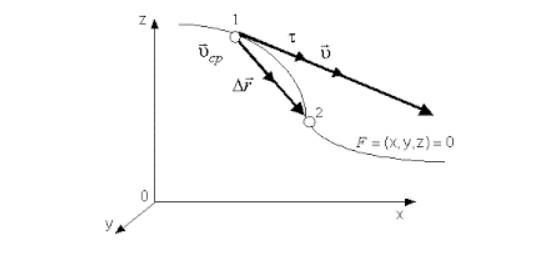
Рисунок . Перемещение и мгновенная скорость в системах криволинейных координат
При сферических координатах предположим, что , то получим , представленную в такой форме:
, где .
Мгновенной скоростью называют значение производной от функции перемещения по времени в заданный момент, связанной с элементарным перемещением соотношением
Дан закон прямолинейного движения точки . Определить ее мгновенную скорость через секунд после начала движения.
Решение
Мгновенной скоростью принято называть первую производную радиус-вектора по времени. Тогда ее запись примет вид:
.
Ответ: .
Движение материальной точки задается уравнением . Вычислить момент времени , когда точка прекратит движение, и ее среднюю путевую скорость .
Решение
Вычислим уравнение мгновенной скорости, подставим числовые выражения:
.
Ответ: заданная точка остановится по прошествии секунд; значение средней скорости равняется .




