- 24 июля 2025
- 8 минут
- 8 988
Основные понятия кинематики
Статью подготовили специалисты образовательного сервиса Zaochnik.
Кинематика − это раздел механики, который рассматривает движение тел без объяснения вызывающих его причин.
Механическое движение тела − это изменение положения данного тела в пространстве относительно других тел во времени.
Как мы сказали, механическое движение тела относительно. Движение одного и того же тела относительно разных тел может быть разным.
Для характеристики движения тела указывается, по отношению к какому из тел рассматривается это движение. Это будет тело отсчета.
Система отсчета − система координат, которая связана с телом отсчета и временем для отсчета. Она позволяет определить положение передвигающегося тела в любой отрезок времени.
В единицей длины выступает метр, а единицей времени – секунда.
У каждого тела есть определенные размеры. Разные части тела расположены в разных пространственных местах. Но в большинстве задач механики не нужно указывать положение отдельных частей тела. Если размеры тела маленькие в сравнении с расстояниями до остальных тел, тогда заданное тело считается его материальной точкой. Таким образом поступают при изучении перемещения планет вокруг Солнца.
Механическое движение называют поступательным, в случае если все части тела перемещаются одинаково.
Поступательное движение наблюдается у кабин в аттракционе «Колесо обозрения» или у автомобиля на прямолинейном участке пути.
При поступательном движении тела его также рассматривают в качестве материальной точки.
Материальная точка − это тело, размерами которого при заданных условиях можно пренебречь.
Материальная точка в механике
Термин “материальная точка” имеет важное значение в механике.
Траектория движения тела − некоторая линия, которую тело или материальная точка описывает, перемещаясь во времени от одной точки до другой.
Местонахождение материальной точки в пространстве в любой временной отрезок (закон движения) определяют, используя зависимость координат от времени или зависимость от времени радиус-вектора , проведенного от начала координат до заданной точки. Наглядно это представлено на рисунке
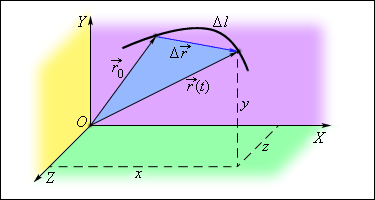
Рисунок Определение положения точки при помощи координат и и радиус-вектора – радиус-вектор положения точки в начальный момент времени.
Перемещение тела – это направленный отрезок прямой, который соединяет начальное положение тела с его дальнейшим положением. Перемещение является векторной величиной.
Пройденный путь равняется длине дуги траектории, преодоленной телом за определенное время . Путь является скалярной величиной.
Если движение тела рассматривается в течение довольно короткого отрезка времени, тогда вектор перемещения оказывается направленным по касательной к траектории в заданной точке, а его длина равняется преодоленному пути.
В случае небольшого промежутка времени преодоленный телом путь практически совпадает с модулем вектора перемещения . При перемещении тела по криволинейной траектории модуль вектора движения все время меньше пройденного пути (рисунок ).
Рисунок Пройденный путь и вектор перемещения при криволинейном движении тела.
и – это начальная и конечная точки пути.
Определение средней и мгновенной скорости движения тела. Основные формулы кинематики
Для описания движения в физике введено понятие средней скорости: .
Физиков больше интересует формула не средней, а мгновенной скорости, которая рассчитывается как предел, к которому стремится средняя скорость на бесконечно маленьком промежутке времени , то есть .
В математике данный предел называется производная и обозначается или .
Мгновенная скорость тела в каждой точке криволинейной траектории направлена по касательной к траектории в заданной точке. Отличие между средней и мгновенной скоростями демонстрирует рисунок
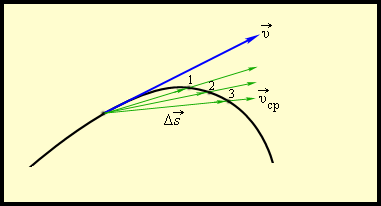
Рисунок Средняя и мгновенная скорости. – перемещения за время соответственно. При .
При перемещении тела по криволинейной траектории скорость меняется по модулю и по направлению. Изменение вектора скорости за какой-то маленький промежуток времени задается при помощи вектора (рисунок ).
Вектор изменения скорости за короткий промежуток времени раскладывается на составляющие: , которая направлена вдоль вектора (касательная составляющая) и , которая направлена перпендикулярно вектору (нормальная составляющая).
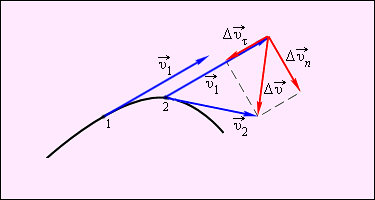
Рисунок Изменение вектора скорости по величине и по направлению. – изменение вектора скорости за промежуток времени .
Мгновенное ускорение тела – это предел отношения небольшого изменения скорости к короткому отрезку времени , в течение которого изменялась скорость: .
Направление вектора ускорения , при криволинейном движении, не совпадает с направлением вектора скорости . Составляющие вектора ускорения – это касательные (тангенциальные) и нормальные ускорения (рисунок ).
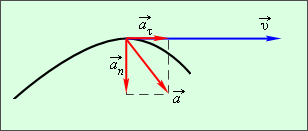
Рисунок Касательное и нормальное ускорения.
Касательное ускорение показывает, как быстро меняется скорость тела по модулю: .
Вектор направлен по касательной к траектории.
Нормальное ускорение показывает, как быстро скорость тела меняется по направлению.
Представим криволинейное движение, как движение по дугам окружностей (рисунок ).
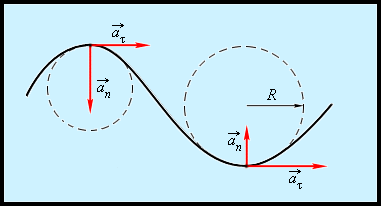
Рисунок Движение по дугам окружностей.
Нормальное ускорение находится в зависимости от модуля скорости и радиуса окружности, по дуге которой тело перемещается в определенный момент времени: .
Вектор все время направлен к центру окружности.
По рисунку видно, модуль полного ускорения равен .
Итак, основные физические величины в кинематике материальной точки – это пройденный путь , перемещение , скорость и ускорение .
Путь – скалярная величина.
Перемещение , скорость и ускорение – векторные величины.
Для того чтобы задать какую-нибудь векторную величину, необходимо задать ее модуль и определить направление. Вектора подчиняются математическим правилам: их можно проектировать на координатные оси, складывать, вычитать и др.




