- 24 июля 2025
- 4 минуты
- 2 263
Относительность движения
Статью подготовили специалисты образовательного сервиса Zaochnik.
Движение тел может быть описано в различных системах отсчета. С точки зрения кинематики они все равноправны, но кинематические характеристики движения, подобные траектории, перемещению и скорости, в разных системах различны.
Величины, зависящие от выбора системы отсчета, в которых производится их измерение, носят название относительных.
Относительность движения
Пускай существуют две системы отсчета. Условно неподвижная система , и система
, которая движется поступательно по отношению к первой системе с некоторой относительной скоростью . Система может быть, к примеру, связана с Землей, а система – с движущейся по рельсам платформой, как это проиллюстрировано на рисунке
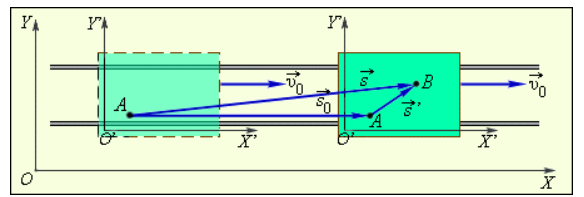
Рисунок Сложение перемещений относительно разных систем отсчета.
Пускай за некоторое время человек передвинулся по платформе из точки в точку . В таком случае, относительно платформы его перемещение соответствует вектору , а перемещение платформы относительно Земли вектору .
С помощью рисунка можно заметить, что перемещение человека относительно Земли будет соответствовать вектору представляющему собой сумму векторов и :
.
Когда одна из систем отсчета поступательно движется относительно другой (как это изображено на рисунке ) с постоянной скоростью , приведенное выражение принимает следующий вид:
.
Классический закон сложения скоростей
Если разобрать перемещение за малый отрезок времени , то разделив обе части этого уравнения на , а после перейдя к пределу при , получим:
.
В данной формуле представляет собой скорость тела в так называемой «неподвижной» системе отсчета , а – скорость тела в «движущейся» системе .
Скорости и в некоторых случаях условно называют абсолютной и относительной скоростями, а скорость – переносной скоростью.
Приведенное выше соотношение выражает классический закон сложения скоростей, формулирующийся следующим образом:
Абсолютная скорость тела эквивалентна векторной сумме его переносной и относительной скоростей и движущейся системы отсчета.
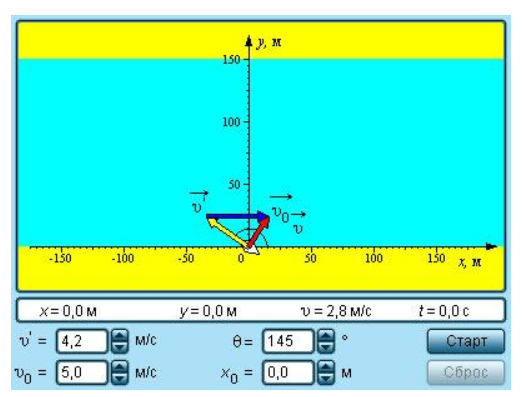
Рисунок Модель относительности движения.
Ускорение тела в системах отсчета
Подробнее рассмотрим тему ускорений тела в разных системах отсчета. В условиях равномерного и прямолинейного движений систем отсчета друг относительно друга ускорения тела в двух приведенных системах равны, , что следует из классического закона сложения скоростей. Действительно, любое изменение undefined относительной скорости тела будет эквивалентно изменению его абсолютной скорости, если является вектором, модуль и направление которого неизменны на протяжении всего времени. Соответственно:
.
Перейдя к пределу , получим .
В условиях ускоренного передвижения систем отсчета друг относительно друга, ускорения тела в разных отличны друг от друга. Когда вектора относительной и переносной скоростей параллельны друг другу, закон сложения скоростей может быть записан в скалярной форме, то есть:
.
В подобном случае каждое движение производится вдоль прямой линии. Скорости и требуется рассматривать в качестве проекций абсолютной, относительной и переносной скоростей на ось . Они представляют из себя алгебраические величины, то есть им следует присваивать необходимые знаки (плюс или минус), в соответствии с направлением их движения.




