Поступательное и вращательное движение

Содержание:

Автор: Роман Адамчук

Преподаватель физики

Движение твердого тела разделяют на виды:

поступательное;
вращательное по неподвижной оси;
плоское;
вращательное вокруг неподвижной точки;
свободное.

Первые два из них – простейшие, а остальные представляют как комбинацию основных движений.

Поступательное криволинейное движение. Угол поворота тела

Определение 1

Поступательным называют движение твердого тела, при котором любая прямая, проведенная в нем, двигается, оставаясь параллельной своему начальному направлению.

Прямолинейное движение является поступательным, но не всякое поступательное будет прямолинейным. При наличии поступательного движения путь тела представляют в виде кривых линий.

Поступательное криволинейное движение. Угол поворота тела

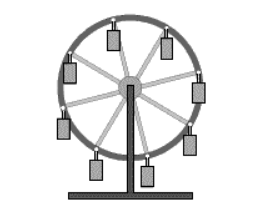
Рисунок $1$ . Поступательное криволинейное движение кабин колеса обзора

Теорема 1

Свойства поступательного движения определяются теоремой: при поступательном движении все точки тела описывают одинаковые траектории и в каждый момент времени обладают одинаковыми по модулю и направлению значениями скорости и ускорения.

Следовательно, поступательное движение твердого тела определено движением любой его точки. Это сводится к задаче кинематики точки.

Определение 2

Если имеется поступательное движение, то общая скорость для всех точек тела $\vec{υ}$ называется скоростью поступательного движения, а ускорение $\vec{a}$ - ускорением поступательного движения. Изображение векторов $\vec{υ}$ и $\vec{a}$ принято указывать приложенными в любой точке тела.

Понятие о скорости и ускорении тела имеют смысл только при наличии поступательного движения. В других случаях точки тела характеризуются разными скоростями и ускорениями.

Определение 3

Вращательное движение абсолютно твердого тела вокруг неподвижной оси – это движение всех точек тела, находящихся в плоскостях, перпендикулярных неподвижной прямой, называемой осью вращения, и описывание окружностей, центры которых располагаются на этой оси.

Чтобы определить положение вращающегося тела, необходимо начертить ось вращения, вдоль которой направляется ось $A z$ , полуплоскость – неподвижную, проходящую через тело и движущуюся с ним, как показано на рисунке $2$ .

Поступательное криволинейное движение. Угол поворота тела

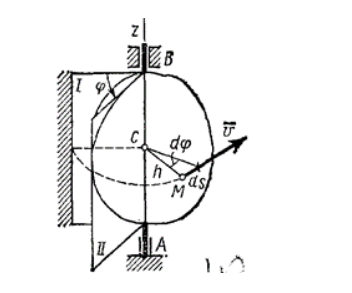
Рисунок $2$ . Угол поворота тела

Положение тела в любой момент времени будет характеризоваться соответствующим знаком перед углом $φ$ между полуплоскостями, который получил название угол поворота тела. При его откладывании, начиная от неподвижной плоскости (направление против хода часовой стрелки), угол принимает положительное значение, против плоскости – отрицательное. Измерение угла производится в радианах. Для определения положения тела в любой момент времени следует учитывать зависимость угла $φ$ от $t$ , то есть $φ = f (t)$ . Уравнение является законом вращательного движения твердого тела вокруг неподвижной оси.

При наличии такого вращения значения углов поворота радиус-вектора различных точек тела будут аналогичны.

Вращательное движение твердого тела характеризуется угловой скоростью $ω$ и угловым ускорением $ε$ .

Уравнения вращательного движения получают из уравнений поступательного, используя замены перемещения $S$ на угловое перемещение $φ$ , скорость $υ$ на угловую скорость $ω$ , а ускорение $a$ на угловое $ε$ .

Вращательное и поступательное движение. Формулы

Поступательное	Вращательное
Равномерное
$s = υ \cdot t$	$φ = ω \cdot t$
$υ = c o n s t$	$ω = c o n s t$
$a = 0$	$ε = 0$
Равнопеременное
$s = υ_{0} t \pm \frac{a t^{2}}{2}$	$φ = ω_{0} t \pm \frac{ε \cdot t^{2}}{2}$
$υ = υ_{0} \pm a \cdot t$	$ω = ω_{0} \pm ε \cdot t$
$a = c o n s t$	$ε = c o n s t$
Неравномерное
$s = f (t)$	$φ = f (t)$
$υ = \frac{d s}{d t}$	$ω = \frac{d φ}{d t}$
$a = \frac{d υ}{d t} = \frac{d^{2} s}{d t^{2}}$	$ε = \frac{d ω}{d t} = \frac{d^{2} φ}{d t^{2}}$

Задачи на вращательное движение

Пример 1

Дана материальная точка, которая движется прямолинейно соответственно уравнению $s = t^{4} + 2 t^{2} + 5$ . Вычислить мгновенную скорость и ускорение точки в конце второй секунды после начала движения, среднюю скорость и пройденный за этот промежуток времени путь.

Дано: $s = t^{4} + 2 t^{2} + 5$ , $t = 2 с$ .

Найти: $s; υ; <υ>; α$ .

Решение

$s = 2^{4} + 2 \cdot 2^{2} + 5 = 29 м$ .

$υ = \frac{d s}{d t} = 4 t^{3} + 4 t = 4 \cdot 2^{3} + 4 \cdot 2 = 37 м / с$ .

$<υ> = \frac{∆ s}{∆ t} = \frac{29}{2} = 14, 5 м / с$ .

$a = \frac{d υ}{d t} = 12 t^{2} + 4 = 12 \cdot 2^{2} + 4 = 52 м / с^{2}$ .

Ответ: $s = 29 м; υ = 37 м / с; <υ> = 14, 5 м / с; α = 52 м / с^{2}$

Пример 2

Задано тело, вращающееся вокруг неподвижной оси по уравнению $φ = t^{4} + 2 t^{2} + 5$ . Произвести вычисление мгновенной угловой скорости, углового ускорения тела в конце $2$ секунды после начала движения, средней угловой скорости и угла поворота за данный промежуток времени.

Дано: $φ = t^{4} + 2 t^{2} + 5$ , $t = 2 с$ .

Найти: $φ; ω; <ω>; ε$ .

Решение

$φ = 2^{4} + 2 \cdot 2^{2} + 5 = 29 р а д$ .

$ω = \frac{d φ}{d t} = 4 t^{3} + 4 t = 4 \cdot 2^{3} + 4 \cdot 2 = 37 р а д / с$ .

$<ω> = \frac{∆ φ}{∆ t} = \frac{29}{2} = 14, 5 р а д / с$ .

$ε = \frac{d ω}{d t} = 12^{2} + 4 = 12 \cdot 2^{2} + 4 = 52 р а д / с^{2}$ .

Ответ: $φ = 29 р а д; ω = 37 р а д / с; <ω> = 14, 5 р а д / с; ε = 52 р а д / с^{2}$ .

Курсовая работа по физике

от 5 дней/ от 2160 р.

Реферат по физике

от 1 дня/ от 840 р.

Решение задач по физике

от 1 дня/ от 150 р.