- 24 июля 2025
- 6 минут
- 6 313
Система отсчета
Статью подготовили специалисты образовательного сервиса Zaochnik.
Система отсчета – это совокупность тела отсчета, со связанной с ним системой координат и прибором для измерения времени.
Что такое система отсчета. Афинная и декартовая системы координат
Если рассматривать все системы отсчета относительно кинематики – они аналогичные. В кинематике не указываются преимущества одной системы отсчета при сравнении с другой. Для удобства решения выбирается наиболее приемлемая система.
Чтобы описать пространство, в котором происходит движение материальной точки, система отсчета связывается с пространственной системой координат.
Системой пространственных координат называют совокупность определений, которая может реализовать метод координат, то есть определение положения точки или тела с помощью чисел или символов.
Числа, способные указать положение выбранной точки в трехмерном пространстве, называются координатами этой точки.
Аффинная система координат – это три линейно независимых вектора (координатных осей), выходящие из одной точки, то есть из начала отсчета.
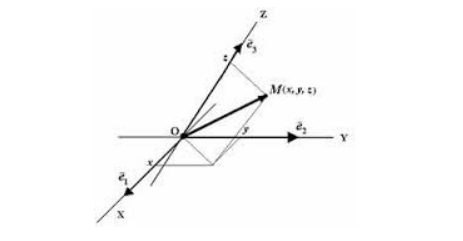
Рисунок . Положение точки в афинной системе координат
Данный случай указывает на то, что определение положения материальной точки в пространстве происходит при помощи радиус-вектора , проведенного через начало координат в заданную точку, движение может быть представлено в виде векторной суммы независимых перемещений вдоль трех пространственных осей выбранной системы координат.
Чаще используется декартова система координат, образованная взаимно перпендикулярными осями . Она применима для описания прямолинейного движения и движения по незамкнутым или нецикличным кривым. Представляет из себя наглядную геометрическую интерпретацию с несложными вычислениями.
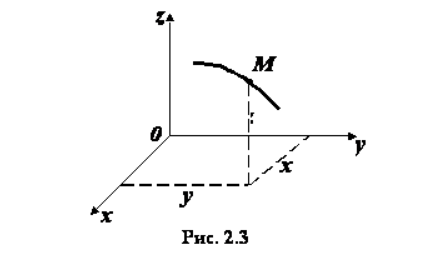
Рисунок . Положение точки в декартовой системе координат
Отложенные от начала координат и вдоль осей единичные векторы называют ортами .
Расположение точки находится в зависимости от значения радиус-вектора , соединяющего начало координат с заданной точкой :
,
являются декартовыми координатами точки или проекциями радиус-вектора на соответствующие оси координат, первая производная которого дает значение мгновенной скорости точки. При известных значениях изменений во времени координат или радиус-вектора, то есть определение , задается характер движения тела в пространстве.
Чтобы однозначно определить положение точки в пространстве, то предполагают наличие зависимости радиус-вектора от параметра (времени) таким образом, что каждому значению параметра соответствует одно значение функции:
.
Данное равенство получило название кинематического уравнения движения материальной точки в векторной форме.
Цилиндрическая и сферическая системы координат
Чтобы описать криволинейное и аффинное движение, применяют криволинейные системы координат, которые упрощают форму записи законов движения тел для облегчения вычисления. Чаще всего используют цилиндрические и сферические системы координат.
Представление цилиндрической системы координат включает в себя трехмерную ось координат, которая является обобщением полярной на трехмерное пространство добавлением третьей координаты, задающей смещение произвольной точки вдоль оси относительно координатной плоскости .
Положение точки может быть определено скалярами и , где – характеризует расстояние от точки к оси , – является углом, образованным проекцией радиус-вектора точки на плоскость с положительным направлением , – проекцией точки на ось .
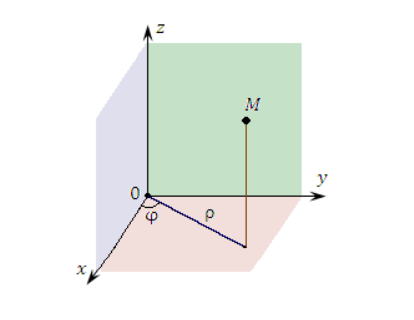
Рисунок . Цилиндрические координаты точки
Связь между декартовыми и цилиндрическими координатами может быть задана при помощи формул:
.
Сферическая система координат характеризуется тройкой скалярных величин, которые определяют положение точки в пространстве, состоящие из длины ее радиус-вектора и двух углов: – угла, образованного проекцией радиус-вектора точки на плоскость с положительным направлением , – угла, располагаемого между радиус-вектором точки и осью .
Необходимо рассмотреть сферическую систему координат , совмещенную с декартовой , причем с имеющимися пределами изменения сферических координат: .
Рисунок показывает, что можно вывести формулы, связывающие сферические и декартовые координаты:
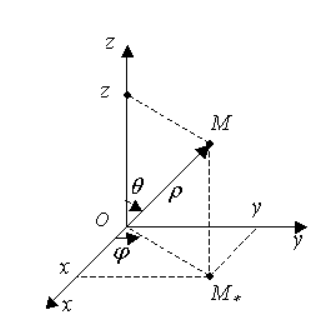
Рисунок . Сферические координаты точки
Имеются другие системы криволинейных координат, с помощью которых возможно нахождение координат заданной точки: параболические, гиперболические, эллиптические и другие.
Система отсчета выбирается индивидуально относительно каждого случая в отдельности, учитывается особенность движения тела, с помощью которой определяется наиболее простой закон движения заданного тела или точки.




