- 24 июля 2025
- 6 минут
- 890
Поле элементарного тока и элементарный ток в магнитном поле
Статью подготовили специалисты образовательного сервиса Zaochnik.
Элементарный замкнутый ток называют линейным, который обтекает поверхность с бесконечно малыми линейными размерами.
Поле элементарного тока
Ранее была получена формула для нахождения векторного потенциала магнитного поля элементарного тока:
, где является магнитным моментом элементарного тока, – радиус-вектором от витка с током до точки, в которой рассматривается поле.
Применив выражение с определением векторного магнитного потенциала , получим:
.
Используя операцию для формулы , которая определяет магнитную индукцию элементарного замкнутого тока, имеем:
.
Элементарный ток в магнитном поле. Контур с током в однородном магнитном поле
Следует выявить характер поведения элементарного тока при его помещении во внешнее магнитное поле. Допустим, что поле однородно, то есть . На такой контур будет действовать сила Ампера, вычисляемая в соответствии с законом, тогда:
, где сила тока и вектор магнитной индукции были вынесены за знак интеграла по причине их постоянства. Формула содержит векторное произведение, тогда значение интеграла .
Уравнение справедливо для контуров любой формы и при любом его расположении относительно направления линий поля. Следовательно, однородное магнитное поле содержит результирующую силу, равную нулю (, при ).
Значение вращающего момента , создаваемого силами, приложенными к контуру относительно некоторой точки , однородного магнитного поля равняется:
, где является магнитным моментом элементарного контура, – положительной нормалью к контуру. Тогда модуль будет иметь вид:
, где – угол между векторами и .
При условии магнитных сил, действующих на отдельные участки контура, не пытающихся повернуть или сдвинуть его, производят растягивание контура в плоскости. Случай говорит о сжатии контура с током в магнитном поле.
Для увеличения угла между векторами индукции магнитного поля и вектором магнитного момента элементарного тока на должна совершиться работа против сил магнитного поля, которая равняется:
.
Работа выполняется на увеличении потенциальной энергии , которой обладает контур с током в магнитном поле:
.
После нахождения интеграла получаем:
.
Если предположить, что в , то:
.
При параллельном ориентировании векторов и получаем минимум потенциальной энергии, иначе говоря, положение устойчивого равновесия. является не полной потенциальной энергией контура с током, а только ее частью, обусловленной вращательным моментом.
Найти работу , которая должна быть совершена внешними силами для поворота контура с током относительно его оси, проходящей через середину его противоположных сторон на угол . При наличии в нем постоянного тока контур легко устанавливается в магнитном поле с индукцией . Значение стороны квадрата равно .
Решение
Для вычисления механического момента, действующего на контур, необходимо использовать формулу:
, где является углом между векторами и . Из условия следует, что контур с имеющейся силой тока находится в равновесии в поле с индукцией. Это говорит о значении момента силы, действующего на контур, равного нулю: .
Если задействовать внешнюю силу на контур, то ее работа по повороту контура на угол будет равняться:
.
Произведем подстановку выражения в с :
.
От возьмем интеграл с условием , тогда:
.
Ответ: .
Система имеет два одинаковые контуры с током, как показано на рисунке . Их магнитные моменты равняются и считаются взаимно перпендикулярными. Найти значение механического момента, действующего на контур , при известном между ними расстоянием . Контуры считать элементарными токами.
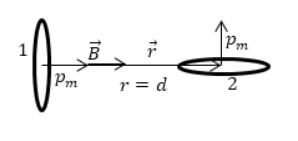
Рисунок
Решение
Создание магнитного поля происходит благодаря элементарному току , индукцию которого находят по формуле:
.
Если учесть значение расстояния между контурами и угол между векторами и , равный нулю, то возможно преобразование выражения . Его запись по модулю примет вид:
.
Вычисление механического момента, действующего на элементарный ток , производится с использованием формулы:
, где угол .
Произведем подстановку для В в :
.
Ответ: .




