- 24 июля 2025
- 6 минут
- 15 482
Поток вектора магнитной индукции
Статью подготовили специалисты образовательного сервиса Zaochnik.
Магнитный поток через площадку (поток вектора магнитной индукции) – это скалярная величина:
с углом между и , обозначаемым , является нормалью к площадке .
Формула магнитного потока
равняется количеству линий магнитной индукции, пересекающих площадку , как показано на рисунке . Поток магнитной индукции по формуле принимает положительные и отрицательные значения. Его знак зависит от выбора положительного направления нормали к площадке . Зачастую положительное направление нормали связано с направлением обхода контура током. За такое направление берут поступательное перемещение правого винта во время его вращения по току.
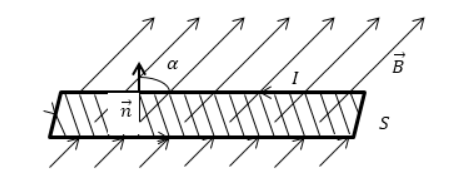
Рисунок
В чем измеряется магнитный поток
В случае неоднородности магнитного поля не будет плоской, а плоскость может быть разбита на элементарные площадки , рассматриваемые в качестве плоских, поле которых также считается однородным. Определение магнитного потока производится через эту поверхность. Запись примет вид:
.
Нахождение полного потока через поверхность :
.
Основной единицей измерения магнитного потока в системе СИ считаются веберы . .
Связь магнитного потока и работы сил магнитного поля
Элементарная работа , совершаемая силами магнитного поля, выражается через элементарное изменение потока вектора магнитной индукции :
.
Если проводник с током совершает конечное перемещение, сила тока постоянна, то работа сил поля равняется:
с , обозначаемым потоком через контур в начале перемещения, является потоком через контур в конце перемещения.
Теорема Гаусса для магнитного поля
Значение суммарного магнитного потока через замкнутую поверхность равняется нулю:
.
Выражение является справедливым для любых магнитных полей. Данное уравнение считается аналогом теоремы Остроградского-Гаусса в электростатике в вакууме:
.
Запись говорит о том, что источник магнитного поля – это не магнитные заряды, а электрические токи.
Дан бесконечно длинный прямой проводник с током , недалеко от которого имеется квадратная рамка. По ней проходит ток с силой . Сторона рамки равна . Она располагается в одной плоскости с проводом, как показано на рисунке . Значение расстояния от ближайшей стороны рамки до проводника равняется . Найти работу магнитной силы при удалении рамки из поля. Считать токи постоянными.
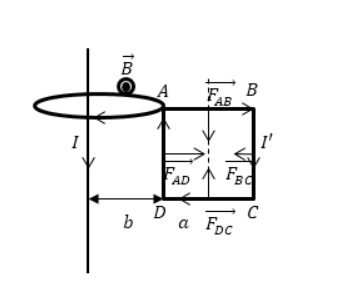
Рисунок
Решение
Индукция магнитного поля длинного проводника с током в части, где расположена квадратная рамка, направляется на нас.
Следует учитывать нахождение рамки с током в неоднородном поле, что означает убывание магнитной индукции при удалении от провода.
За основу возьмем формулу магнитного потока и работы, которая их связывает:
, где принимают за силу тока в рамке, – за поток через квадратную рамку при расстоянии от ее стороны к проводу равняющимся . . Это объясняется тем, что конечное положение рамки вне магнитного поля, как дано по условию. Отсюда следует, запись формулы изменится:
.
Перейдем к нормали и выберем ее направление к квадратному контуру относительно нас, используя правило правого винта. Отсюда следует, что для всех элементов поверхности, ограниченной при помощи контура квадратной рамки, угол между нормалью и вектором равняется . Запись формулы потока через поверхность рамки на расстоянии от провода примет вид:
, значение индукции магнитного поля бесконечно длинного проводника с током силы будет:
.
Отсюда следует, что для нахождения всего потока из потребуется:
.
Произведем подстановку формулы в . Искомая работа равняется:
.
Ответ: .
Найти силу, действующую на рамку, из предыдущего примера.
Решение
Для нахождения искомой силы, действующей на квадратную рамку с током в поле длинного провода, предположим, что под воздействием магнитной силы рамка смещается на незначительное расстояние . Это говорит о совершении силой работы, равной:
.
Элементарная работа может быть выражена как:
.
Произведем то же с силой, применяя формулы . Получаем:
.
Используем выражение, которое было получено в примере :
.
Произведем подстановку в . Имеем:
.
Каждый элемент контура квадратной рамки находится под воздействием сил (силы Ампера). Отсюда следует, что на рамку действует силы, причем на стороны и равные по модулю и противоположные по направлению. Выражение принимает вид:
, то есть их сумма равняется нулю. Тогда значение результирующей силы, приложенной к контуру, запишется:
.
Используя правило левой руки, получаем направление этих сил вдоль одной прямой в противоположные стороны:
.
Произведем поиск силы , действующей на сторону , применив формулу , где :
.
Значение будет:
.
Для нахождения искомой силы:
.
Ответ: . Магнитные силы выталкивают рамку с током до тех пор, пока она находится в первоначальной ориентации относительно поля провода.




