Закон электромагнитной индукции Фарадея и его формулировка в дифференциальной форме

Условие: проволочный контур помещен в магнитное поле. В нулевой момент времени он пронизывает поток магнитной индукции, равный ${\Phi }_1$ и уменьшающийся после этого до $0$. Найдите величину заряда, проходящего по цепи.

Решение

Начнем с определения мгновенного значения ЭДС. Это можно сделать с помощью формулы:

${\epsilon }_i=-\frac{d\Phi }{dt}$.

Вспомним закон Ома. Согласно ему, мгновенное значение силы тока может быть записано в следующем виде:

$I=-\frac{1}{R}\frac{d\Phi }{dt}$.

Полное сопротивление цепи здесь обозначено буквой $R$.

Для нахождения заряда, идущего по цепи, нам пригодится выражение:

$q=\int Idt$.

Поставим эти выражения в нужную формулу и получим:

$q=-\frac{1}{R}{\int }_{{\Phi }_1}^{0}d\Phi =\frac{\Phi }{R}$.

Автором этой формулы является Фарадей. Он эмпирически подтвердил прямую пропорциональность величины заряда, идущего по цепи, количеству линий магнитной индукции, пересекающей проводник, и его обратную пропорциональность величине сопротивления в цепи.

Ответ: $q=\frac{\Phi }{R}$.

Условие: квадратная рамка со стороной a помещена в одну плоскость с проводником, сила тока которого равна $l$. Она движется поступательно с постоянной скоростью $v$ в направлении, обозначенное на иллюстрации ниже. Вычислите ЭДС индукции как функцию ${\epsilon }_i$ от расстояния $x$.

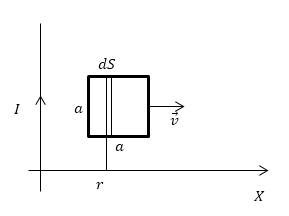
Рисунок $1$

Решение

Найти ответ можно с помощью закона Фарадея.

${\epsilon }_i=-\frac{d\Phi }{dt}$.

Для получения искомой функции $E_i\left(x\right)$ нам нужно построить функцию $Ф\left(x\right)$. Бесконечный проводник с током создает магнитное поле, которое может быть выражено так:

$B=\frac{{\mu }_{0}I}{2\pi r}$.

Расстояние до точки рассмотрения здесь обозначено буквой $r$.

Для решения нам нужно также выделить площадь рамки. Выразим ее такой формулой:

$dS=adr$.

С учетом приведенных выше выражений, а также того факта, что $\overrightarrow{B}\perp \overrightarrow{S}$, мы можем найти величину элементарного магнитного потока, проходящего через элемент квадратной рамки, так:

$d\Phi =BdS=\frac{{\mu }_{0}I}{2\pi r}adr$.

Далее вычисляем величину полного потока, учитывая, что $x\le r\le x+a$:

$\Phi ={\int }_x^{x+a}\frac{{\mu }_{0}I}{2\pi r}adr=\frac{{\mu }_{0}Ia}{2\pi }\ln \frac{x+a}{x}$.

После этого переходим к нахождению ЭДС индукции с помощью закона Фарадея и выражения для магнитного потока, выведенного ранее:

$$\begin{gathered} {\epsilon }_i=-\frac{d\Phi }{dx}·\frac{dx}{dt}=-\frac{{\mu }_{0}Ia}{2\pi }·\frac{x}{x+a}(x^{-1}-(x+a\left)x^{-2}\right)·\upsilon = \\ =-\frac{{\mu }_{0}Ia}{2\pi }·\frac{x}{x+a}\left(\frac{x-x-a}{x^2}\right)=\frac{{\mu }_{0}I{a}^2\upsilon }{2\pi (x+a)x}. \end{gathered}$$

Ответ: ${\epsilon }_i=\frac{{\mu }_{0}I{a}^2\upsilon }{2\pi (x+a)x}$.