Гармонические колебания

Колебательные движения. Формулы

Такие движения относят к явлениям с разной физической природой с подчинением общим закономерностям. Запись колебания тока в электрической цепи и математического маятника производится одним и тем же уравнением. Различная природа колебательных движений позволяет рассматривать их с единой точки зрения, исходя из общности закономерностей.

Когда в заданной среде атомы располагаются очень близко или молекулы испытывают силовое воздействие, наблюдается возбуждение механических колебаний. Это говорит о том, что процесс будет иметь конечную скорость, зависящую от свойств среды, которая распространяется от точки к точке. Так возникают механические волны. Явный пример – звуковые волны в воздухе.

Волновые процессы и колебания разной природы имеют много общего, а их распространение может быть описано аналогичными математическими уравнениями. Это подтверждает единство материального мира.

Гармонические колебания. Определение

В механике предусмотрено движение поступательно, вращательно и с наличием колебаний.

Функция $x=f\left(t\right)$ объясняет закон движения тела с наличием колебаний. При графическом изображении дается представление о протекании колебательного процесса во времени. Рисунок $2.1.1$ наглядно показывает принцип простых колебательных систем груза на пружине или математического маятника.

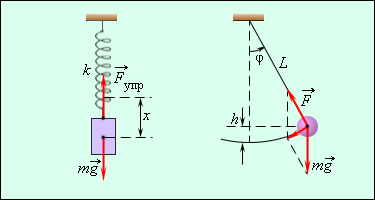
Рисунок $2.1.1.$ Механические колебательные системы.

Механические колебания подразделяют на свободные и вынужденные.

Частота гармонических колебаний показывает их количество, совершаемое за единицу времени, измеряемая в герцах $\left(Г\right)$. Связь с циклической частотой $\omega$ и периодом $T$ выражается с помощью формулы:

$\omega =2\pi f=\frac{2\mathrm{\pi }}{T}$.

Рисунок $2.1.2$ показывает гармонические колебания тел с разными положениями тел. Данный эксперимент наблюдается в специальных условиях при наличии периодических вспышек освещения, называемого стробоскопическим. Для изображения векторов скорости тела в разные моменты времени используют стрелки.

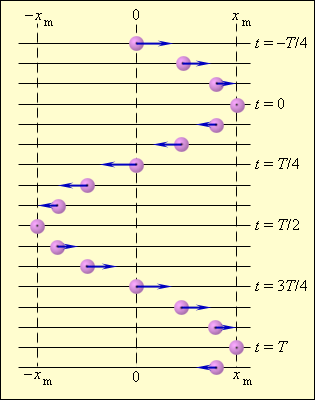
Рисунок $2.1.2.$ Стробоскопическое изображение гармонических колебаний. Начальная фаза ${\phi }_0=0$. Интервал времени между последовательными положениями тела $\tau = \frac{T}{12}$.

На графике $2.1.3.$ показаны изменения, происходящие во время гармонического процесса, при изменении амплитуды колебаний $x_m$, или периода $Т$ (частоты $f$), или начальной фазы ${\phi }_0$.

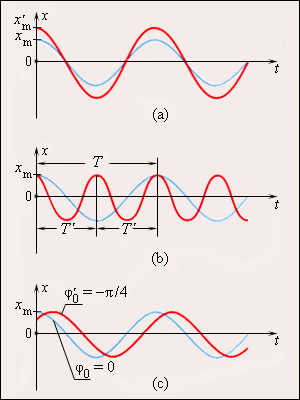
Рисунок $2.1.3.$ Во всех трех случаях для синих кривых ${\phi }_0=0$: $a$ – красная кривая отличается от синей только большей амплитудой $(x{\text{'}}_m>x_m)$; $b$ – красная кривая отличается от синей только значением периода $(T\text{'}=\frac{T}{2})$; $с$ – красная кривая отличается от синей только значением начальной фазы $\left( {\phi }_0^{\text{'}}=-\frac{\pi }{2} рад\right)$.

Гармонический закон

Если колебания совершаются вдоль прямой $Ох$, тогда направление вектора скорости аналогично. Определение скорости движения тела $\upsilon ={\upsilon }_x$ определяют из выражения $\upsilon =\frac{∆x}{∆t}; \left(∆t\to 0\right)$.

Отношение $\frac{∆x}{∆t}$ при $∆t\to 0$ математика трактует как вычисление производной функции $x\left(t\right)$ за определенное время $t$. Обозначение принимает вид $\frac{dx \left(t\right)}{dt}, x\text{'}\left(t\right)$ или $\dot{x}$.

Гармонический закон движения записывается в качестве $x=x_m\cos (\omega t+{\phi }_0)$. После вычисления производной формула приобретает вид:

$\upsilon =\dot{x}\left(t\right)=-\omega x_m\sin (\omega t+{\phi }_0)=\omega x_m\cos \left(\omega t+{\phi }_0+\frac{\mathrm{\pi }}{2}\right)$.

Слагаемое $+\frac{\mathrm{\pi }}{2}$ считают изменением начальной фазы. Достижение максимального значения скорости по модулю $\upsilon =\omega x_m$производится при прохождении тела через положение равновесия, то есть $\left(x=0\right)$. Аналогично определяют ускорение $a=a_x$. Тогда $a=\frac{∆\upsilon }{∆t}, \left(∆t\to 0\right)$. Отсюда следует, что $a$ равняется производной функции $\upsilon \left(t\right)$ за время $t$ или второй производной функции $x\left(t\right)$. Подставив выражения, получим

$a=\dot{\upsilon }\left(t\right)=\ddot{x}\left(t\right)=-{\omega }^2{x}_m\cos (\omega t+{\phi }_0)=-{\omega }^{2}x\left(t\right)$.

Наличие отрицательного знака указывает на то, что ускорение $a\left(t\right)$ имеет противоположный смещению $x\left(t\right)$ знак. Исходя из второго закона Ньютона, сила, которая заставляет совершать колебательные движения, направляется в сторону положения равновесия $\left(x=0\right)$.

На рисунке $2.1.4$ изображены графики, где имеются зависимости скорости, ускорения, совершающие гармонические колебания.

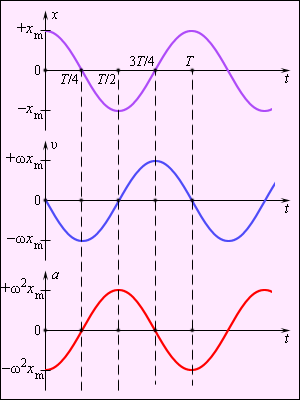
Рисунок $2.1.4.$ Графики координаты $x \left(t\right)$, скорости $\upsilon \left(t\right)$ и ускорения $a \left(t\right)$ тела, совершающего гармонические колебания.

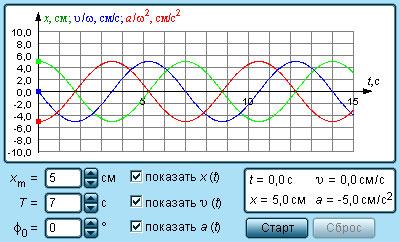
Рисунок $2.1.5.$ Модель гармонических колебаний.