- 24 июля 2025
- 5 минут
- 2 119
Свободные колебания. Математический маятник
Статью подготовили специалисты образовательного сервиса Zaochnik.
При наличии механических колебаний происходит периодическое изменение кинетической и потенциальной энергии. Обращение в ноль кинетической энергии и скорости связано с максимальным отклонением тела от положения равновесия. Энергия такого колеблющегося тела достигает максимального значения. Если груз располагается на горизонтальной пружине, то потенциальная энергия считается энергией упругих деформаций пружины. У математического маятника – это энергия в поле тяготения Земли.
Когда тело принимает положение равновесия при движении, это говорит о наличии минимальной его скорости. Тогда кинетическая энергия обладает максимальным значением, а потенциальная – минимальным. По -му закону Ньютона формула силы натяжения записывается как при вертикальном подвешивании тела на нити. Уменьшение потенциальной приводит к увеличению кинетической. Дальнейшее движение показывает, что происходит уменьшение кинетической и увеличение потенциальной.
Гармонические колебания – это пример превращения кинетической энергии в потенциальную и наоборот.
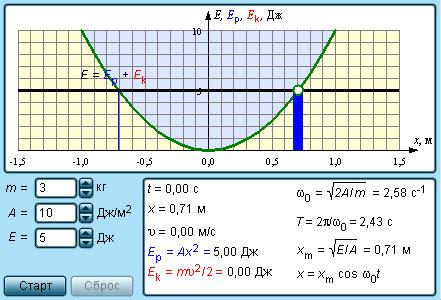
Рисунок Модель превращения энергии при колебаниях.
Математический и пружинный маятник
Когда колебательная система не имеет силы трения, тогда остается неизменной полная механическая энергия.
Формулы, характеризующие груз на пружине:
Выражения при малых колебаниях математического маятника записываются:
Значение является максимальной высотой подъема маятника, и – максимальными значениями отклонения физического маятника от положения равновесия и его скорости.
Для объяснения превращения энергии при свободных механических колебаниях без силы трения приводится иллюстрация.
Если рассматривать колебания с грузом массой на пружине с жесткостью , тогда смещение груза из положения равновесия и его скорость могут изменяться со временем согласно законам:
, где ,
.
Формулы кинетической и потенциальной энергии запишутся так:
,
.
Рисунок показывает два графика функций изменения и . Обе энергии в период колебаний , достигают максимальных значений по два раза. Значение их суммы не изменяется .
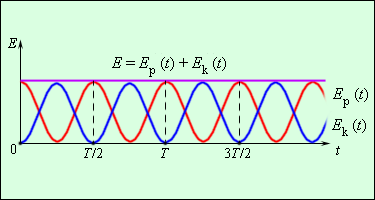
Рисунок Превращения энергии при свободных колебаниях.
Реальные условия для колебательной системы – это наличие воздействия сил трения (сопротивления).
При переходе части механической энергии во внутреннюю энергию теплового движения атомов и молекул колебания становятся затухающими, как показано на рисунке .
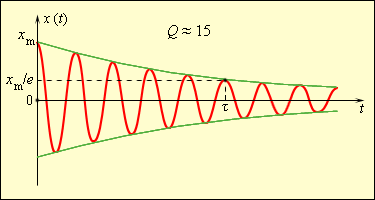
Рисунок Свободные затухающие механические колебания.
Скорость затухания колебаний зависит от величины сил трения.
Частота. Добротность. Формулы
Промежуток времени с уменьшением колебаний в раз называют временем затухания.
Скорость затухания зависит от частоты свободных колебаний, как видно из формулы. При увеличении действия сил трения происходит уменьшение собственной частоты. Если действия силы трения достаточно велико, то изменение частоты становятся заметными.
Колебательная система с затухающими колебаниями характеризуется добротностью .
Определение параметра представляет собой произведение числа полных колебаний за время затухания на значение :
.
Повышение колебательной системы происходит при медленных затуханиях свободных колебаний. На рисунке показано, что имеет значение, приближенное к .
Добротность механических колебательных систем может достигать огромных значений. Для определения колебательной системы применяют формулу:
.
То есть добротность способна характеризовать относительную убыль (затухание) энергии при наличии действия силы трения на данном промежутке времени, равняющемуся одному периоду колебаний.




