
Статью подготовили специалисты образовательного сервиса Zaochnik
Уравнение состояния вещества
- 17 ноября 2023
- 8 минут
- 3 502
Параметры состояния связаны друг с другом. Соотношение, при котором определяется данная связь, называют уравнением состояния данного тела. В самом простом случае равновесное состояние тела определяется значением следующих параметров: давления pp, объема VV и температуры (масса тела или системы, как правило, известна).
Что такое идеальный газ
Уравнение состояния так называемого идеального газа является простым, но достаточно информативным.
Идеальный газ – это газ, в котором пренебрегают взаимодействием молекул между собой.
Идеальными считают разреженные газы. Особенно близки к идеальным газы гелий и водород. Идеальный газ – это упрощенная математическая модель реального газа: молекулы движутся хаотически, а соударения между молекулами и удары молекул о стенки сосуда упругие, не приводящие к потерям энергии в системе. Подобная упрощенная модель весьма удобна, поскольку не требует учета силы взаимодействия между молекулами газа. Множество реальных газов не отличаются в своем поведении от идеального газа в условиях, когда суммарный объем молекул пренебрежимо мал в сравнении с объемом сосуда (то есть при атмосферном давлении и комнатной температуре). Это дает возможность применять уравнение состояния идеального газа для сложных расчетов.
Уравнение состояния идеального газа запишем несколько раз (2), (3), (5)(2), (3), (5):
pV=mμRT=νRT (2)pV=mμRT=νRT (2).
Уравнение (2)(2) – уравнение Менделеева-Клапейрона, где mm – это масса газа, μμ – это молярная масса газа, R=8,31 Джмоль·К – это универсальная газовая постоянная, ν – это число молей вещества.
pV=NkT (3),
где N – это количество молекул газа в массе m, k=1,38·10-23 ДжК, постоянная Больцмана, определяющая «долю» газовой постоянной, которая приходится на 1 молекулу и
N=mNAμ (4),
NA=6,02·1023 моль-1 – это постоянная Авогадро.
Если поделить в (4) обе части на V, то получаем следующий вид записи уравнения состояния идеального газа:
p=nkT (5),
где n=NV – это количество частиц в единице объема или же концентрация частиц.
Что такое реальный газ
Рассмотрим теперь более сложные системы: неидеальные газы и жидкости.
Реальный газ – это газ, между молекулами которого наблюдаются заметные силы взаимодействия.
Необходимо учитывать, что в неидеальных, плотных газах взаимодействие молекул высоко. Известно, что взаимодействие молекул очень сильно усложняет физическую картину, потому точную формулу уравнения состояния неидеального газа не получается записать в простом виде. В данном случае прибегают к приближенным формулам, найденным полу-эмпирическим путем. Самая удачная формула – это уравнение Ван-деp-Ваальса.
Взаимодействие молекул обладает сложным характером. На достаточно больших расстояниях между молекулами действуют силы притяжения. С уменьшением расстояния силы притяжения вначале растут, однако потом уменьшаются и преобразуются в силы отталкивания. Притяжение и отталкивание молекул будем рассматривать и учитывать отдельно. Уравнение Ван-дер-Ваальса, которое описывает состояние одного моля реального газа, имеет вид:
(p+aV2μ)(Vμ-b)=RT (6),
где aV2μ – это внутреннее давление, обусловленное силами притяжения между молекулами, b – это поправка на собственный объем молекул, учитывающая действие сил отталкивания между молекулами, при этом:
b=NA23πd3 (7),
где d – это диаметр молекулы. Значение a рассчитывается по формуле:
a=-2πN2A∫∞dWp(r)r2dr (8),
где Wp(r) – это потенциальная энергия притяжения 2-х молекул.
При увеличении объема значение поправок в уравнении (6) становится менее существенным. И в пределе уравнение (6) превращается в уравнение (2). Это согласовано с тем фактом, что с уменьшением плотности реальные газы по своим характеристикам приближаются к идеальным.
Положительным в уравнении Ван-деp-Ваальса является тот факт, что данное равенство при очень больших плотностях приблизительно описывает также и свойства жидкости, в частности, плохую ее сжимаемость. Потому существует основание предполагать, что уравнение Ван-деp-Ваальса позволяет отразить и переход от жидкости к газу (либо от газа к жидкости).
На рисунке 1 представлена изотерма Ван-дер-Ваальса для некоторого постоянного значения температуры T, которая построена из соответствующего уравнения.
В месте “извилины” (участок КМ) изотерма 3 раза пересекает изобару. На участке
openV1, V2] давление увеличивается с ростом объема.
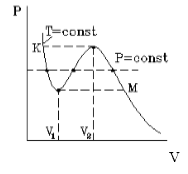
Рисунок 1
Подобная зависимость невозможна. Это означает, что в этой области с веществом происходит что-то необыкновенное. Что именно, не видно в уравнении Ван-деp-Ваальса. Обратимся к опыту. В месте “извилины” на изотерме в состоянии равновесия вещество расслаивается на 2 фазы: жидкую и газообразную. Обе фазы существуют одновременно и находятся в фазовом равновесии. В таком состоянии происходит испарение жидкости и конденсация газа. Процессы протекают с такой интенсивностью, что полностью компенсируют друг друга: объем жидкости и газа со временем не изменяется.
Газ, который находится в фазовом равновесии со своей жидкостью, называется насыщенным паром. Если фазовое равновесие отсутствует, отсутствует также компенсация испарения и конденсации, тогда газ называется ненасыщенным паром.
Что происходит с изотермой в области двухфазного состояния вещества (то есть в месте "извилины" изотермы Ван-деp-Ваальса)? Эксперимент показывает, что в этом месте при изменении объема давление остается неизменным. График изотермы идет параллельно оси V (рисунок 2).
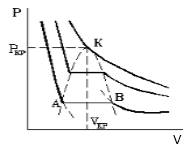
Рисунок 2
С увеличением температуры участок двухфазных состояний на изотермах уменьшается до тех пор, пока не превращается в точку (рисунок 2). Это особая точка К, в которой исчезает разница между жидкостью и паром. Ее называют критической точкой.
Параметры, которые соответствуют критическому состоянию, являются критическими (критическая температура, критическое давление, критическая плотность вещества).
Необходимо найти величину n. В процессе, представленном на рисунке 3, давление p~Tn.
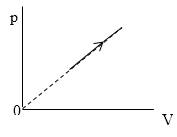
Рисунок 3
Решение
Из графика, приведенного на рисунке 3, запишем уравнение процесса в параметрах p(V):
p=kV или p~V.
С учетом уравнения Менделеева-Клайперона:
pV~T.
Подставив p~V вместо объема, получаем:
p2~T→p~√T
Ответ: n=12.
Моль кислорода охлаждают до -100 °C. Необходимо определить давление, которое оказывает газ на стенки сосуда, если занимаемый газом объем V = 0,1 л. Необходимо также сравнить p с давлением идеального газа pid, если бы кислород вел себя как идеальный газ. Величина постоянных Ван-дер-Ваальса a и b, для кислорода a=0,1358 Па·м6/моль2, b=3,167·10-5м3/моль.
Решение
Из уравнения Ван-Дер-Ваальса имеем:
p=RTVμ-b-aV2μ
Переведем температуру в систему измерения: T=t+273, По условию T=173K, V=0,1 л=10-4м3.
Произведем расчет: p=8,31·173(10-3,2)·10-5-0,1358(10-4)2=75,61·105 (Па).
Для идеального газа:
pid=νRTV
Рассчитаем: pid=1·8,31·17310-4=143·105 (Па).
Ответ: p≈0,53pid.
Сохранить статью удобным способом

