- 24 июля 2025
- 7 минут
- 7 187
Движение тела с переменной массой
Статью подготовили специалисты образовательного сервиса Zaochnik.
Для начала сформулируем, что такое переменная масса.
Переменная масса – это масса тела, которая может меняться при медленных движениях из-за частичных приобретений или потерь составляющего вещества.
Уравнение движения материальной точки с переменной массой
Чтобы записать уравнение движения для тела с такой массой, возьмем для примера движение ракеты. В основе ее перемещений лежит очень простой принцип: она движется за счет выброса вещества с большой скоростью, а также сильного воздействия, оказываемого на это вещество. В свою очередь выбрасываемые газы также оказывают воздействие на ракету, придавая ей ускорение в противоположном направлении. Кроме того, ракета находится под действием внешних сил, таких, как гравитация Солнца и других планет, земная тяжесть, сопротивление среды, в которой она совершает движение.
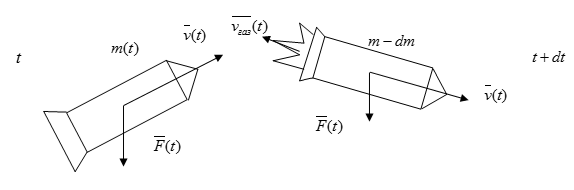
Рисунок
Обозначим массу ракеты в какой-либо момент времени как , а ее скорость как . То количество движения, которая она при этом совершает, будет равно . После того, как пройдет время , обе эти величины получат приращение (соответственно и , причем значение будет меньше ). Тогда количество движения, совершаемого ракетой, станет равно:
.
Нам необходимо учитывать тот момент, что за время также происходит движение газов. Это количество тоже нужно добавить в формулу. Оно будет равно . Первый показатель означает массу газов, которые образуются за указанное время, а второй – их скорость.
Теперь нам нужно найти разность между суммарным количеством движения за время и количеством движения системы во время . Так мы найдем приращение данной величины за время , которое будет равно (буквой обозначена геометрическая сумма всех тех внешних сил, которые действуют в это время на ракету).
В итоге мы можем записать следующее:
.
Поскольку нам важны именно предельные значения , и их производные, приравняем эти показатели к нулю. Значит, после раскрытия скобок произведение может быть отброшено. С учетом сохранения массы получим:
.
Теперь исключим массу газов и получим скорость, с которой газы будут покидать ракету (скорость струи вещества), выражающаяся разностью . Учитывая эти преобразования, можно переписать исходное уравнение в следующем виде:
.
Теперь разделим его на и получим:
.
Уравнение Мещерского
Форма полученного уравнения точно такая же, как у уравнения, выражающего второй закон Ньютона. Но, если там мы имеем дело с постоянной массой тела, то здесь из-за потери вещества она постепенно меняется. К тому же помимо внешней силы нужно учитывать так называемую реактивную силу. В примере с ракетой это будет сила выходящей из нее газовой струи.
Уравнение впервые вывел русский механик И.В. Мещерский, поэтому оно получило его имя. Также его называют уравнением движения тела с переменной массой.
Формула Циолковского
Попробуем исключить из уравнения движения ракеты внешние силы, воздействующие на нее. Предположим, что движение ракеты прямолинейно, а направление противоположно скорости газовой струи . Будем считать направление полета положительным, тогда проекция вектора является отрицательной. Она будет равна . Переведем предыдущее уравнение в скалярную форму:
.
Тогда равенство примет вид:
.
Газовая струя может выходить во время полета с переменной скоростью. Проще всего, разумеется, принять ее в качестве константы. Такой случай наиболее важен для нас, поскольку так уравнение решить намного проще.
Исходя из начальных условий, определим, какое значение приобретет постоянная интегрирования С. Допустим, что в начале пути скорость ракеты будет равна , а масса . Следовательно, из предыдущего уравнения можем вывести:
.
Тогда мы получим соотношения следующего вида:
или .
Это соотношение и является формулой Циолковского.
Она предназначена для расчета запаса топлива, с помощью которого ракета может набрать необходимую скорость. При этом время сгорания топлива не обусловливает величину максимальной скорости ракеты. Чтобы разогнаться до предела, нужно увеличить скорость истечения газов. Для достижения первой космической скорости следует изменить конструкцию ракеты. Она должна быть многоступенчатой, поскольку необходимо меньшее соотношение между требуемой массой топлива и массой ракеты.
Разберем несколько примеров применения данных построений на практике.
Условие: у нас есть космический корабль, скорость которого постоянна. Для изменения направления полета в ней нужно включить двигатель, который выбрасывает газовую струю со скоростью . Направление выброса перпендикулярно траектории корабля. Определите угол изменения вектора скорости при начальной массе корабля и конечной .
Решение
Ускорение по абсолютной величине будет равно , причем .
Значит, уравнение движения будет выглядеть так:
перейдет в .
Поскольку является углом поворота за время , то после интеграции первоначального уравнения получим:
.
Ответ: искомый угол будет равен .
Условие: масса ракеты перед стартом равна . Вычислите высоту, которую она наберет через секунд после начала работы двигателя. Известно, что топливо расходуется со скоростью , а скорость истечения газов постоянна и равна . Поле тяготения Земли можно считать однородным.
Решение
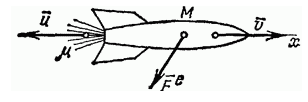
Рисунок
Начнем с записи уравнения Мещерского. Оно будет иметь следующий вид:
.
Здесь и – скорость ракеты в заданный момент времени. Разделим переменные:
.
Теперь решим полученное уравнение с учетом первоначальных условий:
.
С учетом того, что при , у нас получится:
.
Добавим заданные значения и найдем ответ:
.
Ответ: через секунд высота ракеты будет составлять .




