Элементы релятивисткой динамики

Содержание:

26 февраля 2023
7 минут
865

Преподаватель физики

Принцип относительности Эйнштейна утверждает инвариантность всех законов природы по отношению к переходу от одной инерциальной системе отсчета к другой. Отсюда следует, что уравнения, которые описывают законы природы, должны быть инвариантны относительно преобразований Лоренца.

Импульс. Релятивистская масса

Во время создания СТО теории, удовлетворяющей данному условию, она подразумевала уже существующую теорию электродинамики Максвелла. Уравнения вышли неинвариантными относительно преобразований Лоренца, что требовало пересмотра и уточнения законов механики.

Для этого Эйнштейн основывался на требованиях выполнимости закона сохранения импульса и закона сохранения энергии в замкнутых системах. Чтобы он выполнялся во всех инерционных системах отсчета, следовало изменить определение импульса тела.

Определение 1

Классический импульс $\vec{p} = m \vec{ν}$ заменяют релятивистским $\vec{p}$ с массой $m$ и скоростью движения $\vec{ν}$ . Запись принимает вид:

$\vec{p} = \frac{m \vec{ν}}{\sqrt{1 - \frac{ν^{2}}{c^{2}}}} = \frac{m \vec{ν}}{\sqrt{1 - β^{2}}}$ .

Если данное определение задействовать при решении, то закон сохранения суммарного импульса частиц выполнится во всех инерциальных системах, в которых есть связь с преобразованиями Лоренца. Когда $β \to 0$ релятивистский импульс перейдет в классический.

Определение 2

Масса $m$ считается фундаментальной характеристикой частицы. Она не зависит от выбора инерциальной системы отсчета, скорости движения.

Некоторые учебники трактуют это как массу покоя, обозначаемую $m_{0}$ . Позже вводилась релятивистская масса частицы $\frac{m_{0}}{\sqrt{1 - β^{2}}}$ , которая зависела от скорости движения частицы. Современная физика отказывается от данных терминологий.

Определение 3

Запись основного закона релятивистской динамики материальной точки принимает вид, аналогичный второму закону Ньютона:

$\vec{F} = \frac{d \vec{p}}{d t}$ ,

тогда $\vec{p}$ примет значение релятивистского импульса частицы. Отсюда следует

$\vec{F} = \frac{d}{d t} (\frac{m \vec{v}}{\sqrt{1 - \frac{ν^{2}}{c^{2}}}})$ .

Скорость частицы в релятивистской механике не пропорциональна релятивистскому импульсу, то есть скорость изменения не будет пропорциональна ускорению. Отсюда имеем, что сила постоянна по модулю и по направлению, причем не вызывает равноускоренного движения. Если существует одномерное движение вдоль $О х$ , тогда ускорение частицы $a = \frac{d ν}{d t}$ с постоянной $F$ равняется $a = \frac{F}{m} {(1 - \frac{ν^{2}}{c^{2}})}^{\frac{3}{2}}$ .

Движение релятивистской частицы

Определение 4

При росте скорости классической частицы под действием постоянной силы, скорость релятивистской частицы не превышает скорость света $с$ в пустоте.

Это очевидно, так как выполняется закон сохранения энергии релятивистской частицы. Определение $E_{k}$ производится через работу внешней силы, которая необходима для сообщения телу заданной скорости. При разгоне частицы с массой $m$ из состояния покоя до скорости $ν_{0}$ действует постоянная сила, совершающая работу

$A = \int F \cdot d x = \int F \cdot ν \cdot d t = \int \frac{m \cdot α \cdot ν \cdot d t}{{(1 - \frac{ν^{2}}{c^{2}})}^{\frac{3}{2}}}$ .

Так как $α d t = d ν$ , то запись примет вид $E_{k} = A = \int_{0}^{v_{0}} \frac{m \cdot ν \cdot d ν}{{(1 - \frac{ν^{2}}{c^{2}})}^{\frac{3}{2}}}$ .

При вычислении интеграла произойдет упрощение выражения:

$E_{k} = \frac{m c^{2}}{\sqrt{1 - \frac{ν^{2}}{c^{2}}}} - m c^{2}$ .

Интерпретация Эйнштейном первого члена правой части звучит как полная энергия $Е$ движущейся частицы, а второго – энергией покоя $E_{0}$ :

$E = \frac{m c^{2}}{\sqrt{1 - \frac{ν^{2}}{c^{2}}}}, E_{0} = m c^{2} .$

Определение 5

Кинетической энергией $E_{k}$ считают разность между полной $Е$ и энергией покоя $E_{0}$ . Запись принимает вид:

$E_{k} = E - E_{0}$ .

На рисунке $4.5.1$ изображено изменение $E_{k}$ частицы, подчиняющейся классическому и релятивистскому законам.

Движение релятивистской частицы

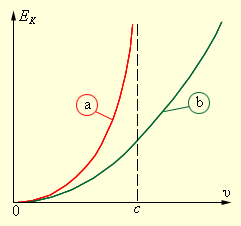
Рисунок $4.5.1 .$ Зависимость кинетической энергии от скорости для релятивистской $(a)$ и классической $(b)$ частиц. При $υ ≪ c$ оба закона совпадают.

Вывод релятивистской механики в том, что масса m, находящаяся в покое, содержит большое количество энергии. Это применяется при ядерной энергии. Если наблюдалось уменьшение массы частицы на $∆ m$ , тогда выделившаяся энергия примет вид $∆ E = ∆ m \cdot c^{2}$ . Проводимые эксперименты дают понять, что существование энергии покоя реальное. Первый, кто подтвердил это, был Эйнштейн. Он использовал отношение, связывающее массу и энергию, полученное при их сравнении. При бета-распаде свободного нейтрона появлялись протон, электрон и антинейтрино с нулевой массой:

$n \to p + e^{-} + \tilde{ν}$ .

Конечные продукты обладали суммарной кинетической энергией, равной $1, 25 \cdot 10^{- 13} Д ж$ .

Определение 6

Масса нейтрона значительно превышает суммарную массу протона и электрона на $∆ m = 13, 9 \cdot 10^{- 31} к г$ . Так как прослеживается уменьшение массы, необходимо использовать соответствующую энергию $∆ E = ∆ m \cdot c^{2} = 1, 25 \cdot 10^{- 13} Д ж$ . Она равняется кинетической энергии релятивистской частицы.

Пример 1

Если взрывается $1 т$ тринитротолуола, то происходит освобождение энергии $4, 2 \cdot 10^{9} Д ж$ , при взрыве мегатонной бомбы – $4, 2 \cdot 10^{15} Д ж$ . Из формулы $m = \frac{E}{c^{2}}$ выходит, что искомая масса – это $46 г$ . При взрыве ядерной бомбы m уменьшается на $50 г$ . То есть масса водородной бомбы при $1$ мегатонне тринитротолуола имеет около $50 к г$ .

Связь между энергией и импульсом релятивистской частицы

Самым важным выводом СТО является закон пропорциональности массы и энергии. Они обладают различными свойствами материи. Масса тела говорит о его инертности или способности вступать в гравитационное взаимодействие с другими телами. Важное свойство энергии – это способность превращения из одной формы в другую во время различных физических процессов, что подтверждает закон сохранения энергии.

Определение 7

Масса и энергия пропорциональны и выражают внутреннюю сущность материи.

Получаем, что формула Эйнштейна $E_{0} = m c^{2}$ выражает фундаментальный закон природы, называемый законом взаимосвязи массы и энергии.

Если скомбинировать выражения $\vec{p} = \frac{m \vec{ν}}{\sqrt{1 - \frac{ν^{2}}{c^{2}}}} = \frac{m \vec{ν}}{\sqrt{1 - β^{2}}}$ и $E = \frac{m c^{2}}{\sqrt{1 - \frac{ν^{2}}{c^{2}}}}$ , то придем к связывающему их соотношению.

Для этого следует переписать эти формулы в упрощенном виде

${(\frac{p^{2}}{m c})}^{2} = \frac{\frac{ν^{2}}{c^{2}}}{1 - \frac{ν^{2}}{c^{2}}}$ ,

${(\frac{E}{m c^{2}})}^{2} = \frac{1}{1 - \frac{ν^{2}}{c^{2}}}$ .

После почленного вычитания получаем $E^{2} = {(m c^{2})}^{2} + {(p c)}^{2}$ .

Следовательно, что для покоящихся частиц энергия фиксируется как $E = E_{0} = m c^{2}$ .

Определение 8

Исходя из соотношения становится понятно, что частица может обладать энергией и импульсом, но не иметь массы, то есть $m = 0$ . Она получила название безмассовой. Для нее используется формула связи энергии и импульса в виде $E = p c$ .

Определение 9

К частицам, которые не имеют массы, относят фотоны, называемые квантами электромагнитного излучения, и нейтрино. Существование безмассовых частиц в покое невозможно, поэтому их движение характеризуется предельной скоростью $с$ .

Курсовая работа по физике

от 5 дней/ от 2160 р.

Реферат по физике

от 1 дня/ от 840 р.

Решение задач по физике

от 1 дня/ от 150 р.