Относительность расстояний

Одно из важных следствий раздела специальной теории относительности - вывод об относительности расстояний. Определение этому понятию звучит следующим образом.

Обозначим длину твердого стержня, измеренную в собственной системе отсчета, где стержень неподвижен, как $l_0$. А также обозначим длиной $l$ стержня в другой системе отсчета, в которой стержень движется со скоростью $\upsilon$. Длина $l$ - это расстояние между концами стержня, которые зафиксированы одновременно по часам данной системы отсчета. В соответствии с теорией относительности справедливо следующее равенство:

$l-l_0\sqrt{1-{\beta }^2}=\frac{l_0}{\gamma }$, где $\gamma =\frac{1}{\sqrt{1-{\beta }^2}}>1, \beta =\frac{\upsilon }{c}$

Получается, что длина движимого стержня всегда меньше, чем длина недвижимого стержня.

Относительность расстояний (длин) зависит от постоянства скорости света в инерциальных системах и от промежутков времени.

Компьютерный эксперимент измерения относительности расстояний

Представим компьютерную модель, которая проводит эксперимент измерения длины твердого стержня $2$-мя наблюдателями из различных инерциальных систем. При этом один наблюдатель находится в неподвижном состоянии по отношению к стержню, а второй передвигается со скоростью $\upsilon$ вдоль стержня. Эксперимент заключается в замере времени распространения светового импульса от одного конца стержня к другому и в обратную сторону. Обозначим событие $1$, как короткую световую вспышку на одном конце стержня и событие $2$, как возвращение светового импульса к лампе. Временной интервал в своей системе отсчета между $2$-мя событиями равняется

${\tau }_{0 }=\frac{2l_0}{c}$.

В движимой системе отсчета временной интервал между $2$-мя событиями равняется

$\tau =\frac{l}{c-\upsilon }+\frac{l}{c+\upsilon }$.

Из этого следует

$l=l_0·\frac{{\tau }_0}{\tau }=\frac{l_0}{\gamma }$.

С помощью компьютерных экспериментов можно менять относительную скорость систем отсчета. На экране вверху демонстрируется эксперимент измерения собственного времени ${\tau }_0$ между событиями системы, где стержень недвижим. А внизу экрана такой же самый эксперимент выполняет наблюдатель с подвижным стержнем в собственной системе отсчета. Результаты эксперимента, а именно значения времени ${\tau }_0$ и $\tau$ отображаются на часах в одной и второй системах отсчета.

Рассмотрим относительность расстояний более подробно.

Измерение длины движущегося стержня

Допустим, твердый стержень неподвижен в системе отсчета $K\text{'}$, которая движется со скоростью υ относительно системы отсчета $K$ (рис. $4.3.1$). Стержень находится параллельно оси $x\text{'}$.

Какова длина данного стержня, если ее захочет измерить наблюдатель в системе $K$?

Известно, что длина $l$ стержня в системе $K$, относительно которой передвигается стержень, - это расстояние между координатами концов стержня, отмеченными одновременно по часам данной системы. Если мы знаем скорость системы $K\text{'}$ по отношению к системе $K$, тогда измерение длины движущегося стержня сводится к измерению временного интервала: длина $l$ стержня, движущегося со скоростью $\upsilon$, равняется произведению $\upsilon {\tau }_0$ , где ${\tau }_0$ – это временной интервал по часам в системе $K$ между началом стержня и его конца мимо какой-то неподвижной точки (к примеру, точки $A$) в системе $K$ (рис. $4.3.1$). Поскольку в системе $K$ оба события - прохождение начала (событие $1$) и конца (событие $2$) стержня мимо фиксированной точки $A$ - происходят в одной и той же точке, тогда временной промежуток ${\tau }_0$ в системе $K$ - это собственное время. Таким образом, длина $l$ движущегося стержня равняется $l=\upsilon {\tau }_0$.

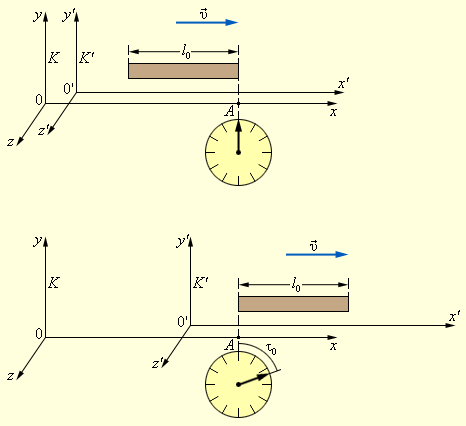
Рисунок $4.3.1.$ Измерение длины движущегося стержня.

Сейчас выведем связь между $l$ и $l_0$. С позиции наблюдателя в системе $K\text{'}$, точка $A$, которая принадлежит системе $K$, передвигается вдоль неподвижного стержня в левую сторону со скоростью υ, поэтому можно записать следующее утверждение:

$l_0=\upsilon \tau$,

где $\tau$ - это временной промежуток между моментами прохождения точки $A$ мимо концов обоих стержня, который измерен по синхронизованным часам в системе $K\text{'}$. Зная зависимость между промежутками времени $\tau$ и ${\tau }_{\mathrm{0:}}$ $\tau =\frac{{\tau }_0}{\sqrt{1-{\beta }^2}}$, запишем следующую формулу:

$l=l_0\sqrt{1-\frac{{\upsilon }^2}{c^2}}=l_0\sqrt{1-{\beta }^2}$

Относительность длины стержня

Мы выяснили, что расстояние - это относительная величина, которая зависит от скорости движения тела в заданной системе отсчета. Сокращение длины не зависит от каких-либо процессов, происходящих в самих телах. Лоренцево сокращение описывает изменение размера подвижного тела по направлению его движения. Если стержень на рис. $4.3.1$ положить перпендикулярно оси $x$ (вдоль нее движется система $K\text{'}$), то длина стержня будет одинакова для наблюдателей двух систем $K$ и $K\text{'}$. Таким образом, всех инерциальные системы равноправны.

Обращаем внимание, что при маленьких скоростях движения $(\upsilon \ll c)$ формулы СТО преобразуются в классические соотношения: $l\approx l_0$ и $\tau \approx {\tau }_0$. Так, классические представления, которые лежат в основе механики Ньютона и которые сформировали на основе многолетнего опыта наблюдения над медленными движениями, в специальной теории относительности соответствуют предельному переходу при $\beta =\frac{\upsilon }{с}\to 0$. Здесь прослеживается принцип соответствия.