- 24 июля 2025
- 7 минут
- 1 801
Тепловой двигатель
Статью подготовили специалисты образовательного сервиса Zaochnik.
Термодинамика возникла как наука с основной задачей – созданием наиболее эффективных тепловых машин.
Тепловая машина или тепловой двигатель – это периодически действующий двигатель, совершающий работу за счет получения теплоты.
Обычно совершение работы в тепловом двигателе производится газом при его расширении. Газ, находящийся в нем, получил название рабочего тела. Зачастую его заменяют на воздух или водяные пары. Расширение газа происходит по причине повышения его температуры и давления.
Устройство, от которого рабочее тело получает тепло , называю нагревателем.
Это понимается как расширение от объема к , затем сжатие до первоначального объема. Чтобы значение совершаемой работы за цикл было больше нуля, необходимо температуру и давление увеличить и сделать больше, чем при его сжатии. То есть при расширении телу сообщается определенное количество теплоты, а при сжатии отнимается. Значит, кроме нагревателя тепловой двигатель должен иметь холодильник, которому рабочее тело может отдавать тепло.
Рабочее тело совершает работу циклично. Очевидно, изменение внутренней энергии газа в двигателе равняется нулю. Если при расширении от нагревателя к рабочему телу передается теплота в количестве , то при сжатии теплота рабочего тела передается холодильнику по первому закону термодинамики, учитывая, что , то значение работы газа в круговом процессе запишется как:
.
Отсюда теплота . Выгодность двигателя определяется по количеству выделенной и превращенной теплоты, полученной от нагревателя, в работу. Его эффективность характеризуется коэффициентом полезного действия (КПД), определяющимся как:
.
Запись уравнения при учитывании примет вид:
, КПД всегда.
Машина, отбирающая от тела с меньшей температурой определенное количество теплоты и отдающая его телу с наиболее высокой температурой с , получила название холодильной машины.
Данная машина должна совершить работу в течение цикла. Эффективность холодильной машины определяется по холодильному коэффициенту, вычисляемому:
.
КПД необратимого теплового двигателя всегда меньше, чем работающего по обратимому циклу.
КПД теплового двигателя
Французским инженером Саади Карно была установлена зависимость КПД теплового двигателя от температуры нагревателя и холодильника . Форма конструкции теплового двигателя и выбор рабочего тела не влияет на КПД идеальной тепловой машины:
.
Любой реальный тепловой двигатель может обладать КПД .
Принцип работы теплового двигателя
Идеальная машина, модель которой разработал Карно, работает по обратимому циклу, состоящему из двух изотерм и двух адиабат , изображенная на рисунке . В качестве рабочего тела выбран идеальный газ. Прохождение адиабатного процесса происходит без подвода и отвода тепла.
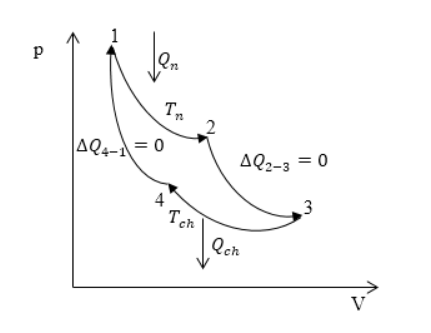
Рисунок
Участок характеризуется сообщением рабочему телу от нагревателя с температурой количества тепла . При изотермическом процессе запись примет вид:
, где являются энтропиями в соответствующих точках цикла из рисунка .
Видно, что участок характеризуется отдачей тепла холодильнику с температурой идеальным газом, причем количество теплоты равняется получению газом теплоты , тогда:
.
Выражение, записанное в скобках в , указывает на приращение энтропии процесса .
Принцип действия тепловых двигателей КПД
Произведем подстановку , в определение КПД теплового двигателя и получаем:
.
В выведенном выражении не выполнялось предположений о свойствах рабочего тела и устройстве теплового двигателя.
По уравнению видно, что для увеличения КПД следует повышать и понижать . Достижение значения абсолютного нуля невозможно, поэтому единственное решение для роста КПД – увеличение .
Задача по созданию теплового двигателя, совершающего работу без холодильника, очень интересна. В физике она получила название вечного двигателя второго рода. Такая задача не находится в противоречии с первым законом термодинамики. Данная проблема считается неразрешимой, как и создание вечного двигателя первого рода. Этот опытный факт в термодинамике приняли в качестве постулата – второго начала термодинамики.
Рассчитать КПД теплового двигателя с температурой нагревания и температурой холодильника, равной . Считать тепловую машину идеальной.
Решение
Необходимо применение выражения для КПД теплового двигателя, которое записывается как:
.
Используя систему , получим:
Подставляем числовые значения и вычисляем:
.
Ответ: КПД теплового двигателя равняется .
Найти КПД цикла, представленного на рисунке , если в его пределах объем идеального газа проходит изменения раз. Считать рабочим веществом газ с показателем адиабаты .
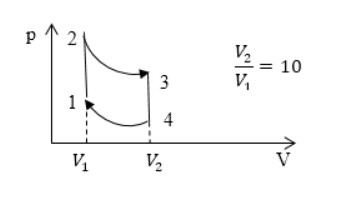
Рисунок
Решение
Основная формула для вычисления КПД, необходимая для решения данной задачи:
.
Получения тепла газом происходит во время процесса :
, где потому как является изохорным процессом. Отсюда следует:
.
Процесс, когда газ отдает тепло, обозначается как , считается изохорным . Формула примет вид:
.
Адиабатные процессы проходят без подвода и отвода тепла.
Произведем подстановку полученных количеств теплоты в выражение для КПД, тогда:
.
Следует применить уравнение для адиабаты процессу :
.
Используем выражение для адиабаты процесса :
.
Перейдем к нахождению разности температур :
.
Произведем подстановку из в :
.
Ответ: КПД цикла равняется .




