Дифракционная картина в дальней зоне как Фурье-образ дифракционного объекта

2 декабря 2023
5 минут
351

Преподаватель физики

Когда распространение волны $E_{0}$ идет по $О z$ и попадает на экран, совпадающий с плоскостью $z = 0$ , тогда амплитудный коэффициент пропускания равняется $τ (x, y)$ . Случай указывает на поле волны за экраном, которая проходит через преграду $(E_{τ})$ .

Используя теорему Фурье, функция $E_{τ} (x, y)$ может быть представлена:

Выражение $(2)$ показывает, что световое поле представлено как суперпозиция плоских волн, амплитуды которых обозначены через $F (u, v)$ - пространственный спектр.

Реализация Фурье – образа

При дифрагировании световой волны на большие углы излучение обладает высокими пространственными частотами. Если распространение волны идет по оси $Z$ , то ей соответствует нулевая пространственная частота. То есть для решения задачи Фраунгофера следует обозначить пространственный спектр волнового поля за экраном, определенного уравнением $(1)$ и равного свертке спектров падающей волны $E_{0} (x, y)$ и коэффициента пропускания экрана. Если $E_{0} (x, y)$ считается плоской волной, то не существует зависимости ее поля от поперечных координат, угловой спектр совпадает с угловым спектром пропускания экрана.

Определение 1

Образование изображений и преобразование Фурье – это проявление дифракции.

Картина дифракции Фраунгофера – Фурье образ

Дифракция Фраунгофера наблюдается при выполненном условии для дальней зоны в фокальной плоскости оптической системы.

Значение $l$ определяет расстояние от препятствия (отверстия) до экрана, $b$ - ширину щели (диаметр/радиус).

Возьмем для рассмотрения плоскость $P$ , которой принадлежит излучающая поверхность $S$ . Отсюда получим, что плоскостью наблюдения будет являться $P'$ . Расстояние между этими плоскостями равняется $z$ , как показано на рисунке $1$ .

Картина дифракции Фраунгофера – Фурье образ

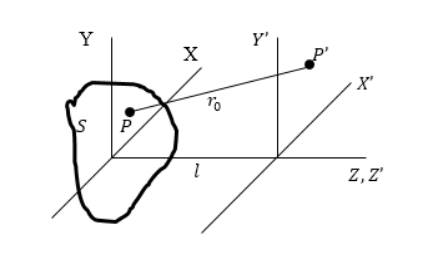
Рисунок $1$

Отметим, что не существует комплексного коэффициента усиления для дифракции Фраунгофера, так как условие пространственной инвариантности поля нарушено.

Примеры Фурье – образов

Пример 1

При совершении дифракции Фраунгофера на круглом отверстии волной, форма сигнала будет в виде круга. Допустим, его радиус равняется $R$ . Запись Фурье – образ сигнала запишется:

$F (u, v) = \frac{J_{1} (R ρ)}{ρ} e^{i u ∆ x + i u ∆ y}$ ,

где выражение $ρ = \sqrt{u^{2} + v^{2}} J_{1} (R ρ)$ является функцией Бесселя первого рода и первого порядка, так как она действительная и четная, $∆ x, ∆ y$ – смещением сигнала по соответствующим осям.

Образ Фурье – считается четным и действительным при условии смещения $∆ x = ∆ y = 0$ . Смещением называют фазовую добавку. При ее наличии модуль Фурье – образа не изменен, отсюда и получаем изображение дифракции, который пропорционален квадрату, сохраняется.

Особым практическим интересом обладает задача о дифракции на круглом отверстии, так как оправы и диафрагмы множества приборов в оптике обладают круглой формой. Для решения такого рода задач применяют цилиндрическую систему координат. Для этого следует использовать двойное интегрирование по радиальной и азимутным переменным.

Результат дифракции – акисально-симметричная картина, обладающая ярким световым пятном в центре, называемым диском Эйри. Он включает в себя около $84 %$ световой энергии.

Пример 2

Была совершена фраунговерова дифракция на квадратном отверстии со стороной
$2 a$ при помощи плоской волны. Форма сигнала – квадрат. Фурье – образ такого сигнала записывается как:

$F (u, v) = \frac{\sin (a u)}{u} \frac{\sin (a v)}{v} e^{i (u ∆ x + v ∆ y)}$ .

Значение $∆ x, ∆ y$ относят к смещению сигнала по соответствующим осям. Функция $\frac{\sin (x)}{x}$ является действительной и четной, как и Фурье – образ при $∆ x = ∆ y = 0$ . Если смещение не равняется нулю, то это влечет за собой появление дополнительных осцилляций без изменения модуля Фурье – образа. Картина дифракции сохраняется и остается прежней.

Пример 3

Дифракция опыта Юнга является дифракцией Фраунгофера плоской волны на двух круглых отверстиях. Тогда запись Фурье – образа такого сигнала примет вид:

$F (u, v) = \frac{J_{1} (R ρ)}{ρ} \{e x p (i u ∆ x_{1} + i v ∆ y_{1}) + e x p (i u ∆ x_{2} + i v ∆ y_{2})\}$ .

Значение $ρ = \sqrt{u^{2} + v^{2}}, J_{1} (R ρ)$ считается за функцию Бесселя $1$ рода и $1$ порядка, $x_{1}, y_{1}; x_{2}, y_{2}$ - за координаты центров кругов. Вид квадрата Фурье – образа – это кольца, соответствующие кругу радиуса $R$ . Они модулируются при помощи полос, находящихся на одинаковом расстоянии. Полосы располагаются перпендикулярно линии, соединяющей центры кругов. Расстояние между полосами обратно пропорционально расстоянию между кругами.