Интерференция световых волн

Первый научный эксперимент проявления интерференции света

Первый научный эксперимент по наблюдению интерференции света провел в лабораторных условиях И. Ньютон. Ученый рассматривал интерференционную картину, которая возникала при отражении света в тонкой воздушной прослойке между плоской стеклянной пластиной и плосковыпуклой линзой большого радиуса кривизны. Наблюдение Ньютона графически изображено на рис. $3.7.1.$

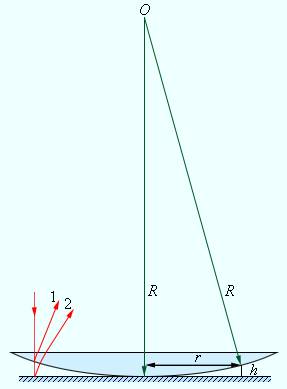
Рисунок $3.7.1.$ Наблюдение колец Ньютона. Интерференционная картина возникает при сложении волн, отразившихся от $2$-х сторон воздушной прослойки. «Лучи» $1$ и $2$ – направления распространения волн;
$h$ – толщина воздушного зазора.

Рисунок $3.7.2.$ Кольца Ньютона в зеленом и красном свете.

У И. Ньютона не получилось с позиции корпускулярной теории дать объяснение тому, почему возникают кольца. Но ученый понимал, что это имеет отношение к какой-то периодичности световых процессов$$.

Интерференционный опыт Юнга

В $1802$ году ученый Юнга провел первый интерференционный опыт, которому есть подтверждение в волновой теории света. В данном эксперименте свет от источника – узкой щели $S$ попадал на экран с
$2$-мя близко расположенными друг к другу щелями $S_1$ и $S_2$, как показано на рис. $3.7.3.$ Минуя каждую из щелей, световой пучок уширялся из-за дифракции, а потому на белом экране $Э$ световые пучки, которые прошли через щели $S_1$ и $S_2$, перекрывались. В месте перекрытия световых пучков находится интерференционная картина, выступающая в виде чередующихся светлых и темных полос.

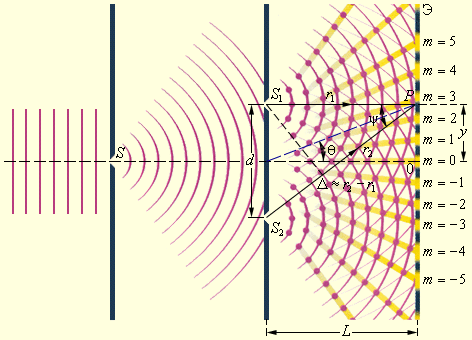
Рисунок $3.7.3.$ Схема интерференционного опыта Юнга.

Ученый Юнг - первый, кто догадался, что невозможно увидеть интерференцию, если сложить волны от $2$-х независимых источников. Потому в его эксперименте щели $S_1$ и $S_2$, которые по принципу Гюйгенса можно рассматривать в качестве источников вторичных волн, освещались светом одного источника $S$. Если симметрично расположить щели, то вторичные волны от источников $S_1$ и $S_2$ находятся в фазе, однако волны проходят до точки наблюдения $P$ различные расстояния $r_1$ и $r_2$. Можно сделать вывод, что фазы колебаний, которые создаются волнами от источников $S_1$ и $S_2$ в точке $P$, различные. Следует, что задача об интерференции волн - это задача о сложении колебаний одинаковой частоты, но с различными фазами.

Приборы, которые могли бы следить за быстрыми изменениями поля световой волны в оптическом диапазоне, не существуют. Наблюдаемая величина - это поток энергии, прямо пропорциональный квадрату амплитуды электрического поля волны.

Путем простых тригонометрических вычислений можно прийти к следующему выражению для интенсивности результирующего колебания в точке $P$:

$I=A^2=a_1^2+a_2^2+2a_1{a}_2 \cos k∆=I_1+I_2+2\sqrt{I_1{I}_2} \cos k∆ (*)$,

где $\Delta =r_2–r_1$ – это разность хода.

Из данного выражения можно сделать вывод, что интерференционный максимум (то есть светлая полоса) достигается в таких точках пространства, в которых $\Delta =m\lambda (m=0, \pm 1, \pm 2, ...)$. Причем $I_{max}=(a_1+a_2{)}^2=I_1+I_2$. Интерференционный минимум (то есть темная полоса) достигается при $\Delta =m\lambda +\frac{\lambda }{2}$. Минимальное значение интенсивности $I_{min}=(a_1–a_2{)}^2<I_1+I_2$. Рис. $3.7.4$ наглядно показывает, как распределяется интенсивность света в интерференционной картине, смотря от того, каким будет ход $\Delta$.

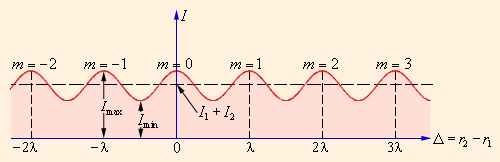
Рисунок $3.7.4.$ Распределение интенсивности в интерференционной картине. Целое число $m$ – это порядок интерференционного максимума.

Предположим, что если $I_1=I_2=I_0$, то есть длина $1$ и $2$ световой волны одинакова, то выражение $(*)$ выглядит следующим образом:

$I=2I_0(1+\cos k\Delta ) (**).$

В данном случае $I_{max}=4I_0, I_{min}=0$.

Формулы $(*)$ и $(**)$ - универсальные. Они подходят для любой интерференционной схемы, в которой складываются $2$ монохроматические волны одинаковой частоты.

Обозначим в схеме Юнга смещение точки наблюдения от плоскости симметрии $y$, тогда в случае, когда $d\ll L$ и $y\ll L$ (как правило, в оптических экспериментах данные условия соблюдаются), можно приблизительно получить:

$∆\approx d·\theta \approx \frac{d·y}{L}$.

Разность хода $\Delta$ меняется на одну длину волны $\lambda$ при смещении от одного интерференционного максимума к другому, то есть на расстояние, эквивалентное ширине интерференционной полосы $\Delta l$. Получается,

$\frac{d·∆l}{L}=\lambda$ или $∆l=\frac{L·\lambda }{d}\approx \frac{\lambda }{\psi }$,

где $\psi$ – это угол схождения «лучей» в точке наблюдения $P$.

Далее данный термин будет упоминаться без кавычек.

При рассмотрении эксперимента И. Ньютона (рис.$3.7.1$) при нормальном падении волны на плоскую поверхность линзы разность хода примерно равняется удвоенной толщине $2h$ воздушного промежутка между линзой и плоскостью. Если радиус кривизны $R$ линзы огромен в сравнении с $h$, можно приблизительно получить формулу:

$h\approx \frac{r^2}{2R}$,

где $r$ – это смещение от оси симметрии. Вычисляя разность хода, следует учитывать, что волны $1$ и $2$ отражаются при различных условиях. $1$-я волна отражается от границы стекло–воздух, а $2$-я – от границы воздух–стекло. В последнем варианте фаза колебаний отраженной волны изменяется на $\pi$, что равно увеличению разности хода на $\frac{\lambda }{2}$. А потому

$∆=2h+\frac{\lambda }{2}\approx \frac{r^2}{R}+\frac{\lambda }{2}$.

При условии $r=0$, то есть в центре (точка соприкосновения) $\Delta =\frac{ \lambda }{2}$; потому в центре колец И. Ньютона всегда находится интерференционный минимум (зрительно это выглядит, как темное пятно). Радиусы $r_m$ следующих темных колец вычисляются по формуле

$r_m=\sqrt{m\lambda R}$.

По данной формуле рассчитывается длина световой волны $\lambda$ при известном радиусе кривизны $R$ линзы.

Проблема когерентности волн

С помощью теории Юнга объясняются интерференционные явления, которые возникают при сложении $2$-х монохроматических волн одинаковой частоты. Но сегодняшний опыт показывает, что интерференцию света на самом деле наблюдать не так-то просто. Если комнату осветить $2$ одинаковыми лампочками, то в любой точке сложатся интенсивности света и здесь не будет никакой интерференции. Тогда появляется вопрос, когда нужно сложить напряженности (учитывая фазовые соотношения), а когда – интенсивности волн, то есть квадраты напряженностей полей? К сожалению, теория интерференции монохроматических волн не дает ответ на данный вопрос.

Реальные световые волны - не строго монохроматические. По фундаментальным физическим причинам излучение всегда происходит статистически (или случайно). Атомы источника света излучают независимо друг от друга в какие-то моменты времени, и каждый атом излучает свет очень короткий промежуток времени $(\tau \le {10}^{–8} с)$. Итоговое излучение источника света в определенный момент времени складывается из вкладов огромного количества атомов. Спустя время порядка $\tau$ совокупность излучающих атомов полностью обновляется. Потому суммарное излучение будет с другой амплитудой и, что очень важно, с другой фазой. Фаза волны, которая излучается реальным источником света, примерно постоянна только лишь на интервалах времени порядка $\tau$.

Интерференция возникает только лишь при сложении когерентных колебаний, то есть колебаний, которые относятся к одному цугу. Хоть и фазы каждого колебания также подвергаются случайным временным изменениям, но данные изменения одинаковы, потому разность фаз когерентных колебаний постоянна. В данном случае наблюдается устойчивая интерференционная картина и, значит, выполняется принцип суперпозиции полей. При сложении некогерентных колебаний разность фаз - это случайная функция времени. В этом случае интерференционные полосы подвергаются беспорядочным перемещениям из одной стороны в другую, и за время $\Delta t$ их регистрации, которая в оптических экспериментах существенно превышает время когерентности $(\Delta t\gg \tau )$, наблюдается полное усреднение. Глаз, фотопластинка или фотоэлемент фиксирует в точке наблюдения усредненную величину интенсивности, равную сумме интенсивностей $I_1+I_2$ этих колебаний. Здесь соблюдается закон сложения интенсивностей.

Итак, интерференция возникает только лишь при сложении когерентных колебаний. Волны, которые создают в точке наблюдения когерентные колебания, тоже называют когерентными. Волны от $2$-х независимых источников некогерентны и не дают интерференцию. Ученый Юнг интуитивно догадался для того, чтобы получить интерференцию света нужно волну от источника разделить на $2$ когерентные волны и потом смотреть на экране результат их сложения. Так устроены все интерференционные схемы. Но даже в данном случае интерференционная картина пропадает, если разность хода $\Delta$ превышает длину когерентности $c\tau$.

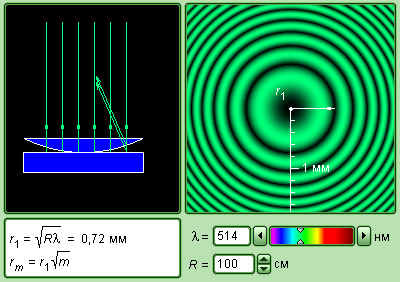
Рисунок $3.7.5.$ Модель кольца Ньютона.

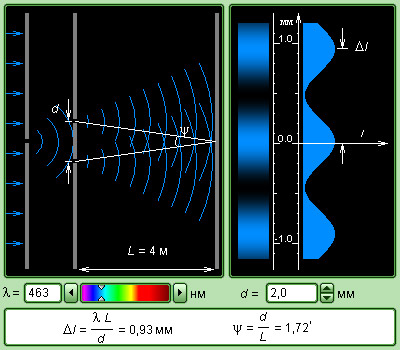
Рисунок $3.7.6.$ Модель интерференционый опыт Юнга.