
Статью подготовили специалисты образовательного сервиса Zaochnik
Спектральные приборы. Дифракционная решетка
- 9 октября 2023
- 12 минут
- 1 291
В состав видимого спектра света включены монохроматические волны с различными длинами. В излучении нагретых объектов (к примеру, нити лампы накаливания) длины волн беспрерывно заполняют весь диапазон видимого света. Данное излучение называют белым светом.
Свет, излучаемый, например, газоразрядными лампами или одним из множества других подобных им приборами, включает в свой состав отдельные монохроматические составляющие с некоторыми выделенными значениями длин волн.
Комплекс монохроматических компонент в излучении называется спектром.
Белый свет имеет непрерывный спектр, излучение источников, в которых он испускается атомами вещества, и дискретный спектр.
Спектральные приборы – это устройства, с помощью которых изучаются спектры излучения источников.
Для разложения излучения в спектр в простейшем спектральном приборе используется призма избраженная на картинке 3.10.1.
Действие призмы базируется на таком явлении, как дисперсия, то есть на привязанности показателя преломления n вещества к длине волны света λ.
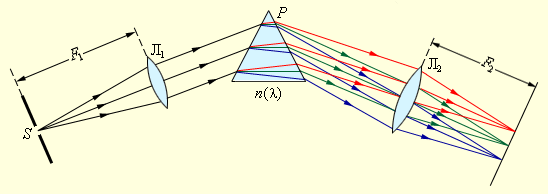
Рисунок 3.10.1. Разложение излучения в спектр с помощью призмы.
Щель S, на которую падает рассматриваемое излучение, располагается в фокальной плоскости линзы Л1. Этот элемент прибора называется коллиматором.
Выходя из линзы, параллельный пучок света падает на призму P. По причине дисперсии, свет различных длин волн излучается из призмы под разнящимися углами. В фокальной плоскости линзы Л2 устанавливают экран или фотопластинку, для фокусировки места излучения. Таким образом, в разных частях экрана появляется проекция входной щели S в свете различных длин волн.
У любого прозрачного твердого вещества (стекло, кварц), из которого изготавливаются призмы, показатель преломления n в диапазоне видимого света уменьшается с возрастанием длины волны λ, из-за чего призма наиболее сильно отклоняет, от их изначального направления, синие и фиолетовые лучи, а красные – наименее. Убывающая без ускорения зависимость n (λ) носит название нормальной дисперсии.
Первый опыт по разложению белого света в спектр осуществил известный физик И. Ньютон в 1672 году.
Дифракционные решетки
В спектральных приборах, относящихся к высокому классу точности, место призм занимают дифракционные решетки. Они представляют из себя периодические конструкции, которые гравируют, посредством использования особой делительной машины, на поверхности стеклянной или металлической пластинки (рис. 3.10.2).
У качественных решеток штрихи, параллельные друг другу, имеют длину около 10 см, где на каждый миллиметр решетки приходится до 2000 штрихов. Причем, общая длина решетки может достигать 10–15 см. Создание подобных решеток требует применения технологий самого высокого класса. Практически используются и более грубые версии решетки с 50 – 100 штрихами на миллиметр, которые нанесены на поверхность прозрачной пленки. В роли дифракционной решетки может применяться небольшая часть компакт-диска или даже осколок граммофонной пластинки.
Рисунок 3.10.2. Дифракционная решетка.
Самый простой тип дифракционной решетки производится из прозрачных участков, то есть щелей, которые разделены непрозрачными промежутками. С помощью коллиматора, на решетку направляется параллельный пучок исследуемого света. Наблюдение проводится в фокальной плоскости линзы, установленной за плоскостью решетки (рис. 3.10.3).
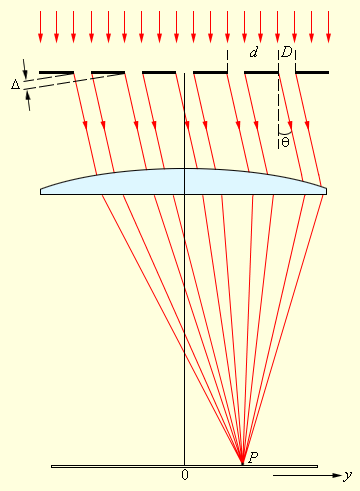
Рисунок 3.10.3. Дифракция света на решетке.
В каждой точке P на экране в фокальной плоскости линзы сходятся лучи, который до линзы являлись параллельными между собой и расходились под некоторым углом θ к направлению падающей волны.
Интерференция волн
Колебание в точке P представляют собой следствие интерференции вторичных волн, которые сходятся в эту точку от разных щелей.
Для того, чтобы в точке P прослеживался интерференционный максимум, разность хода Δ между волнами, который испускают соседние щели, должна быть эквивалентной целому числу длин волн:
∆=d sin θm=mλ (m=0, ±1, ±2,...).
Где d – это период дифракционной решетки, а m – целое число, носящее название порядка дифракционного максимума. В точках экрана, для которых это условие выполнено, расположены главные максимумы дифракционной картины.
В фокальной плоскости линзы, расстояние ym между максимумами нулевого порядка (m=0) и m-го порядка при сравнительно малых углах дифракции равняется:
γm=mλαF,
где F – фокусное расстояние.
Также следует обратить внимание на то, что в каждой точке фокальной плоскости линзы, имеет место интерференция N волн, которые приходят в эту точку от N щелей решетки. Данный феномен является так называемой многоволновой или же «многолучевой» интерференцией.
Распространение световой энергии в плоскости наблюдения значительно отличается от того, которое выходит в обыкновенных «двухлучевых» интерференционных схемах. В главные максимумы все волны приходят в фазе, из-за чего амплитуда колебаний увеличивается в N раз, а интенсивность в N2 раз, относительно колебания, которое провоцирует волна только от одной конкретной щели.
В условиях смещения из главных максимумов, стремительно теряется интенсивность колебаний. Для того, чтобы N волн погасили друг друга, значение разности фаз должно измениться на 2π N, а не на π, как в случае интерференции двух волн.
На рис. 3.10.4 можно увидеть векторную диаграмму колебаний, возбуждаемых волнами от всех N щелей, если сдвиг фаз волн от соседних щелей равен 2π N, а соответствующая разность хода равна отношению λN.
Векторы, иллюстрирующие N колебаний, в данной ситуации формируют замкнутый многоугольник. Следовательно, при переходе из главного максимума в соседний минимум, разность хода Δ=d sin θ смениться на λN. Исходя из данного условия, справедливым будет оценить угловую полуширину δθ главных максимумов:
δ∆=δ(d sin θ)=d cos θ δθ≈d·δθ=λN.
Здесь, дифракционные углы считаются достаточно малыми. Таким образом,
δθ=λNd.
Где Nd – это полный размер решетки. Данное выражение находится в полной симметрии с теорией дифракции в параллельных лучах. Согласно этой теории, дифракционная расходимость параллельного пучка лучей эквивалентна отношению длины волны λ к поперечному размеру препятствия.
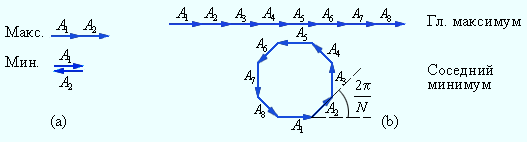
Рисунок 3.10.4. Сложение колебаний в максимуме и минимуме интерференционной картины: a – интерференция двух волн, b – интерференция N волн (N=8).
Из описанного выше, можно сделать однозначный вывод: при дифракции света на решетке главные максимумы крайне узки. Рис. 3.10.5 иллюстрирует изменение остроты главных максимумов при возрастании количества щелей решетки.
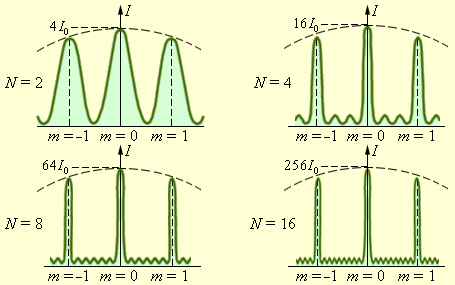
Рисунок 3.10.5. Распределение интенсивности при дифракции монохроматического света на решетках с различным числом щелей. I0 – интенсивность колебаний при дифракции света на одной щели.
Исходя из формулы дифракционной решетки, мы можем заявить, что положение главных максимумов, кроме нулевого, зависит от длины волны λ. По этой причине решетка может разбивать излучение в спектр. Следовательно, она является спектральным прибором. В случае, если на решетку попадает не монохроматическое излучение, то в каждом порядке дифракции, а именно при каждом значении m, проявляется спектр исследуемого излучения.
Также стоит обратить внимание на то, что фиолетовая часть спектра расположена ближе к максимуму нулевого порядка. На рис. 3.10.6 для белого света проиллюстрированы спектры различных порядков. Максимум нулевого порядка остается неокрашенным.
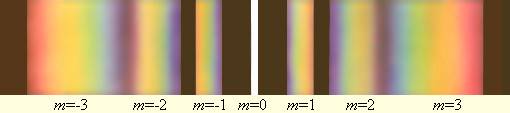
Рисунок 3.10.6. Разложение белого света в спектр с помощью дифракционной решетки.
Используя дифракционную решетку, мы получаем возможность производить крайне точные измерения длины волны. При условии, что период d решетки известен, нахождение искомой величины (длины) приводится к измерению угла θm, соответствующего направлению на выбранной линии в спектре m-го порядка. На практике, чаще всего применяются спектры 1-го или 2-го порядков.
Решетка в любом спектральном порядке (кроме m=0) имеет возможность отсоединить одну волну от другой в случае, если в спектре изучаемого излучения есть две спектральные линии, обладающие длинами волн λ1 и λ2.
Разрешающая способность дифракционной решетки - это одна из основных ее характеристик. Ей характеризуется возможность разделения при использовании решетки двух близких спектральных линий с длинами волн λ и λ+Δλ.
Спектральная разрешающая способность R является отношением длины волны λ к минимальному реальному значению Δλ, то есть: R=λ∆λ
Волновая природа света
Волновая природа света определяет разрешающую способность спектральных приборов, в частности, дифракционной решетки, так же от нее зависит предельное разрешение различных оптических инструментов, которые создают изображение объектов, таких как телескоп, микроскоп и др.
Считается, что если главный максимум для длины волны λ+Δλ отступает от главного максимума для длины волны λ не менее, чем на полуширину главного максимума, т. е. на δθ=λNd, то две ближайшие линии в спектре m-го порядка различимы. Вывод выше является критерием Релея, примененным к спектральному прибору.
Из формулы решетки следует:
dd·cosθ·∆θ=m∆λ или ∆θ=mδ cos θ∆λ≈md∆λ
Где Δθ является угловым расстоянием между двумя главными максимумами в спектре m-го порядка для двух близких спектральных линий с разницей длин волн Δλ. Для упрощения, углы дифракции предполагаются незначительно малыми (cos θ ≈ 1). Уравнивая Δθ и δθ, получаем оценку разрешающей силы решетки:
λNd=md∆λ или R=λ∆λ=mN.
Из описанного выше следует, что предельное разрешение дифракционной решетки может зависеть только от порядка спектра m и от количества периодов решетки N.
Пускай период решетки d=10–3 мм, а ее длина L=10 см.
Решение
В таком случае, N=105.
Исходя из данных показателей, можно с уверенностью сказать, что это хорошая решетка. В спектре 2-го порядка разрешающая способность решетки равна R=2·105. Это указывает на то, что минимально разрешенный диапазон длин волн в зеленой части спектра (т.е. при λ=550 нм) равен Δλ =λ R≈ 2,8·10–3 нм, а предельное разрешение решетки с d = 10–2 м и L = 2 см было бы равным Δλ=1,4·10–1 нм.
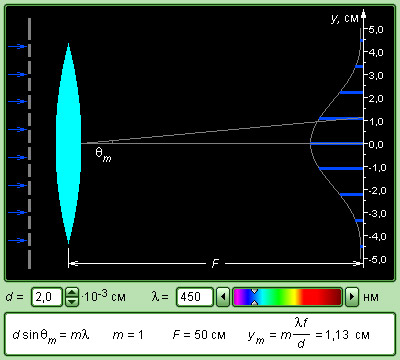
Рисунок 3.10.7. Модель дифракционной решетки.
Сохранить статью удобным способом

