- 24 июля 2025
- 7 минут
- 2 762
Спираль Корню
Статью подготовили специалисты образовательного сервиса Zaochnik.
Интегралы следующего вида: носят название интегралов Френеля. Они вычисляются при помощи численных методов. Также существуют таблицы данных интегралов. Стоит учитывать, что при .
Графически данные таблицы проиллюстрированы как спираль Корню (рис.).
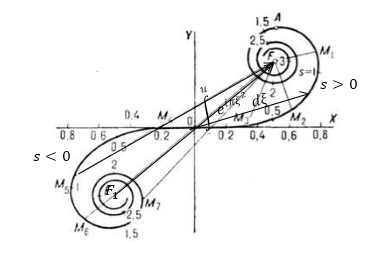
Рисунок
Приведенная спираль включает в свой состав пару закручивающихся вокруг фокусов симметричных ветвей. С помощью верхней ветви изображается действие правой половины фронта, в свою очередь, нижняя ветвь соответствует левой части фронта. Отличие от спирали Френеля вызвано тем, что убывание начальных зон Шустера происходит несколько быстрее, чем убывание зон Френеля.
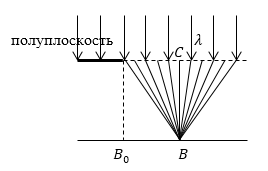
Представим, что путь распространения плоской волны света преграждается непрозрачным плоским экраном с прямым краем. В этом случае левая часть спирали Корню характеризует результат колебаний, которые приходят в точку наблюдения от тех участков поверхности волны (если бы они были открыты), которые лежат левее края непрозрачной полуплоскости. Амплитуда колебаний в точке наблюдения от располагающейся правее края используемого преграждающего экрана волновой поверхности иллюстрируется вектором, который проводится из точки в фокус точку фокуса . Амплитуда колебаний в точке наблюдения от полностью открытой волновой поверхности характеризуется вектором, который проходит от нижнего левого фокуса до верхнего правого, соединяя их.
Рисунок
Спираль Корню используют в качестве метода анализа дифракции. Она дает возможность количественно анализировать распределение интенсивности в картине дифракции.
Применение спирали Корню для нахождения амплитуды колебаний
Для того, чтобы найти амплитуду колебаний в точке наблюдения, которая находится правее , как это изображено на рисунке , от какой-либо полосы волновой поверхности, необходимо построить вектор, замыкающий соответствующий исследуемой полосе участок спирали Корню. Таким образом, выходит следующая схема действий. Каждой точке, принадлежащей спирали Корню, соответствует определенное значение параметра (данный параметр пропорционален длине дуги спирали, которая берет начало в точке . Смотрите рисунок ). Величины параметра указываются на кривой.
Для того, чтобы применять спираль Корню нам необходимо обладать информацией о значении параметра . Его несложно найти, если известно расстояние от точки наблюдения до центра картины. Вычислив ширину первой зоны Шустера , следующим делом с помощью формулы узнаем значение параметра .
Использование спирали Корню в целях нахождения интенсивности света
Рассмотрим пример механизма нахождения распределения интенсивности, применяя спираль Корню. Найдем ее на экране поблизости от края геометрической тени, в условиях дифракции плоской волны от прямого края непрозрачной полуплоскости (рис. ).
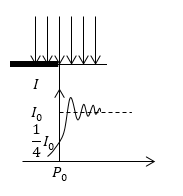
При условии, что точка расположена правее (рис. ), правая часть поверхности волны полностью открыта (от точки ). В этом случае на спирали амплитуда колебаний, в точке наблюдения, соответствует вектору , изображенному на рисунке . Начало приведенного вектора определяется положением точки наблюдения. В ситуации, когда такой точкой является , или же, другими словами, край геометрической тени, то точка начала вектора совпадает с точкой спирали Корню, а его вектор – амплитуда колебаний иллюстрируется в виде вектора , который эквивалентен половине вектора от открытой полностью волновой поверхности. Таким образом, интенсивность света в точке в раза ниже, чем интенсивность при отсутствующих преградах. В условиях перемещения точки наблюдения в правую сторону от точки начало вектора, принадлежащее спирали Корню, производит движение по ее левой ветке, в этом случае слева от точки открываются новые зоны. Как результат амплитуда и интенсивность в точке будут претерпевать изменения от максимума к минимуму. Различие между ними в условиях удаления точек и друг от друга будет постепенно девальвироваться. При этом интенсивность света приближается к величине интенсивности падающего света (рис. ).
В случае, если точка наблюдения совершает перемещение от точки в область геометрической тени, то начало вектора, принадлежащее спирали Корню движется вправо от точки . В этой ситуации длина вектора, а вместе с ней и интенсивность света, монотонно снижается до нуля (рис. ).
Рисунок
Найдите расстояние между первыми двумя максимумами на экране, если картина дифракции наблюдается от края непрозрачной полубесконечной плоскости, которая расположена на расстоянии от экрана. Длина волны света эквивалентна значению .
Решение
Расстояние между максимумами может быть найдено при использовании приведенной ниже формулы:
.
В качестве следующего шага применим формулу для параметра спирали Корню, из которой выразим :
.
Таким образом, для справедливо выражение вида:
.
Проведем вычисления:
.
Ответ: .
Применяя понятие касательной к спирали Корню опишите поведение спирали.
Решение
Пускай угол наклона касательной к спирали Корню в выбранной точке будет равен , в таком случае справедливой будет следующая запись:
.
Формула спирали Корню в параметрическом виде:
.
Из уравнений и следует, что:
.
Если , то . Из этого выходит вывод о том, что кривая Корню в начале координат касается оси . При , кривая Корню уходит вверх. При , , касательная горизонтальна, однако направляется против оси . При , касательная вертикально идет вниз. При , касательная в горизонтальном направлении (исходном).
Ответ: выражение описывает, как спираль Корню обвивается вокруг своих фокусов (рис.). Производя бесконечно много оборотов.




