- 24 июля 2025
- 14 минут
- 4 770
Звук
Статью подготовили специалисты образовательного сервиса Zaochnik.
Перед тем, как приступить к рассмотрению темы, дадим определение такому явлению, как звук.
Звук или звуковые волны – это волны, которые способно воспринять человеческое ухо.
При этом звуковые частоты имеют диапазон: примерно от до .
Инфразвук – звуковые волны, имеющие частоту менее .
Ультразвук – волны звука, имеющие частоту более .
Волнам звукового диапазона свойственно распространяться как в газе, так и в жидкости (продольные волны), и в твердом теле (продольные и поперечные волны). Особенно интересно для науки заниматься изучением распространения звуковых волн в газообразной среде, что по сути есть среда нашего обитания.
Акустика – это направление физики, занимающееся изучением звуковых явлений.
Когда звук получает распространение в газе, атомы и молекулы испытывают колебания вдоль направления распространения волны, следствием чего становится изменение локальной плотности и давления .
Звуковые волны в газе зачастую называют волнами плотности или волнами давления.
В случае простых гармонических звуковых волн, получающих распространение вдоль оси , изменение давления имеет зависимость от координаты и времени , которая записывается так:
.
В аргументе косинуса мы видим два противоположных знака, что имеет отношение к двум направлениям распространения волны. Запишем выражение, которое покажет соотношение таких величин, как круговая частота , волновое число , длина волны , скорость звука (соотношение будет таким же, как применимо для поперечных волн в струне или резиновом жгуте):
.
Одной из ключевых характеристик звука является скорость распространения.
Скорость распространения – величина, описывающая звуковую волну, задаваемая инертными и упругими свойствами среды и определяемая для продольных волн в любой однородной среде при помощи формулы:
.
В указанной формуле является модулем всестороннего сжатия, – средней плотностью среды.
Формула Лапласа
Первые попытки рассчитать значение скорости звука предпринял Ньютон, предположив равенство упругости воздуха атмосферному давлению . В таком случае значение скорости звука в воздушной среде – менее , в то время как истинная скорость звука при нормальных условиях (температура и давление ) равна , а скорость звука при температуре и давлении составит . Лишь по прошествии более ста лет было показано, почему предположение Ньютона не выполняется. Французский физик П. Лаплас указал, что ньютоновское видение равносильно предположению о быстром выравнивании температуры между областями разрежения и сжатия, и невыполнение его связано с плохой теплопроводностью воздуха и малым периодом колебаний в звуковой волне. В действительности между областями разрежения и сжатия газа появляется разность температур, существенным образом влияющая на упругие свойства. Лаплас, в свою очередь, выдвинул предположение, что сжатие и разрежение газа в звуковой волне происходят в соответствии с адиабатическим законом: в отсутствии влияния теплопроводности. В году физик вывел формулу, предназначенную для расчета скорости звуковой волны в воздухе и получившей название формулы Лапласа.
Формула Лапласа для определения скорости звука имеет запись:
.
Где является значением среднего давления в газе, – средней плотности, а есть некоторая константа, находящаяся в зависимости от свойств газа.
В нормальных условиях скорость звука, рассчитанная по формуле Лапласа, равна .
В термодинамике имеется доказательство, что константа γ представляет собой отношение теплоемкостей при постоянном давлении и постоянном объеме .
Формула Лапласа может быть записана несколько иначе, если использовать уравнение состояния идеального газа. Таким образом, окончательный вид формулы для определения скорости звука будет такой:
.
В данной формуле – абсолютная температура, – молярная масса,
– универсальная газовая постоянная. Скорость звука находится в сильной зависимости от свойств газа: скорость звука тем больше, чем легче газ, в котором звуковая волна получает распространение.
Для наглядности приведем некоторые примеры.
Когда звук распространяется в воздушной среде при нормальных условиях: ;
Когда звук распространяется в гелии : ;
Когда звук распространяется в водороде : .
В жидкостях и твердых телах скорость звуковых волн еще больше. В воде, например, (при ), в стали .
Характеристики звуковых волн
Помимо скорости распространения звук имеет и другие характеристики, связанные с восприятием его человеческими органами слуха.
Громкость звука
Рассуждая о том, как человеческое ухо воспринимает звук, в первую очередь мы говорим об уровне громкости, который зависит от потока энергии или интенсивности звуковой волны. А то, как воздействует звуковая волна на барабанную перепонку, зависит от звукового давления.
Звуковое давление – это амплитуда колебаний давления в волне
Природа отлично потрудилась, создавая такое совершенное устройство, как человеческое ухо: оно способно воспринимать звуки в обширнейшем диапазоне интенсивностей. Мы имеем возможность слышать как слабый писк комара, так и грохот вулкана.
Порог слышимости – минимальное значение величины звукового давления, при котором звук этой частоты еще воспринимается человеческим ухом.
Болевой порог – это верхняя граница диапазона слышимости человека; та величина звукового давления, при котором звук вызывает в человеческом ухе ощущение боли.
Порог слышимости представляет собой значение около , т. е. : такой слабый звук характеризуется колебанием молекул воздуха в волне звука с амплитудой всего лишь ! Болевой же порог соответствует значению порядка или . Т.е., человеческое ухо способно к восприятию волн, в которых звуковое давление изменяется в миллион раз. Поскольку интенсивность звука пропорциональна квадрату звукового давления, диапазон интенсивностей оказывается порядка !
Человеческое ухо, восприимчивое к звукам такого огромного диапазона интенсивности, допустимо сравнить с прибором, которым возможно измерить как диаметр атома, так и размеры футбольного поля.
Для общей информированности заметим, что обычным разговорам людей в комнате соответствует интенсивность звука, примерно в раз превышающая порог слышимости, а интенсивность звука на рок-концерте находится очень близко к болевому порогу.
Высота звука
Высота звуковой волны – еще одна характеристика звука, влияющая на слуховое восприятие. Человеческие ухо воспринимает колебания в гармонической звуковой волне как музыкальный тон.
Высокий тон – это звуки с колебаниями высокой частоты.
Низкий тон – это звуки с колебаниями низкой частоты.
Звуки, которые издают музыкальные инструменты, а также звуки голоса человека значимо отличаются друг от друга по высоте тона и по диапазону частот.
К примеру, диапазон наиболее низкого мужского голоса – баса – находится в пределах примерно от
до , а диапазон высокого женского голоса – сопрано – от до .
Октава – это диапазон колебаний звука, который соответствует изменению частоты колебаний в раза.
Скрипка, к примеру, звучит в диапазоне примерно трех с половиной октав ,
а пианино – семи с лишним октав .
Говоря о частоте звука, который извлекается при помощи струн любого струнного музыкального инструмента, будем иметь в виду частоту основного тона. Однако колебания струн содержат также гармоники, частоты которых отвечают соотношению:
.
Таким образом, звучащая струна способна излучать целый спектр волн с кратными частотами. Амплитуды этих волн имеют зависимость от способа возбуждения струны, будь то смычок или молоточек. Эти амплитуды необходимы для придания музыкальной окраски звуку (тембру).
Аналогичный процесс мы наблюдаем, когда звучат духовые музыкальные инструменте. Трубы духовых инструментов служат акустическими резонаторами – акустическими колебательными системами, имеющими способность возбуждаться (резонировать) от звуковых волн определенных частот. Определенные же условия способствуют возникновению внутри трубы стоячей звуковой волны. Рисунок демонстрирует несколько видов стоячих волн (мод) в органной трубе, закрытой с одного конца и открытой с другого. Звучание духовых инструментов, так же, как и струнных, состоит из целого спектра волн с кратными частотами.
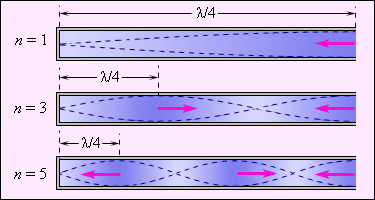
Рисунок Стоячие волны в трубе органа (закрыта лишь с одной стороны). Стрелки указывают направления движения частиц воздуха за один полупериод колебаний.
Музыкальные инструменты необходимо периодически настраивать.
Камертон – устройство для настройки музыкальных инструментов, состоящее из настроенных в резонанс деревянного акустического резонатора и соединенной с ним металлической вилки.
Удар молоточка по вилке вызывает возбуждение всей системы камертона с последующим звучанием чистого музыкального тона.
Гортань певца – по сути тоже акустический резонатор. Рисунок демонстрирует спектры звуковых волн, издаваемых камертоном, струной пианино и низким женским голосом (альтом), звучащими на одной и той же ноте.
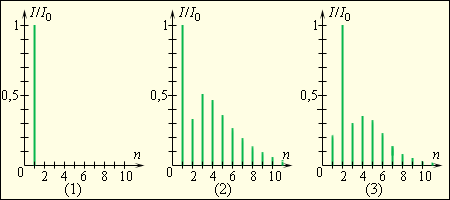
Рисунок Относительные интенсивности гармоник в спектре волну звука при звучании камертона , пианино и низкого женского голоса (альт) на ноте «ля» контроктавы . По оси ординат отложены относительные интенсивности .
Звуковые волны, чьи частотные спектры показаны на рисунке , имеют одну и ту же высоту, но различные тембры.
Биения
Разберем также такое явление, как биения.
Биение – это явление, возникающее, когда две гармонические волны с близкими, но все же имеющими отличия частотами, накладываются друг на друга.
Биения сопровождают, к примеру, одновременное звучание двух струн, имеющих настройки практически одинаковой частоты. Человеческий орган слуха воспринимает биения как гармонический тон с громкостью, периодически изменяющейся во времени. Запишем выражения, показывающие закономерность изменения звуковых давлений и , которые осуществляют воздействие на ухо:
и .
Для удобства примем, что амплитуды колебаний звуковых давлений являются одинаковыми и равны 0.
Согласно принципу суперпозиции полное давление, которое вызывается обеими волнами в каждый момент времени, есть совокупность звуковых давлений, задаваемых каждой волной в тот же момент времени. Запишем выражение, показывающее суммарное воздействие волн, используя тригонометрические преобразования:
,
где , а.
Рисунок отображает, каким образом давления и зависимы от времени . В момент времени оба колебания находятся в фазе, и их амплитуды суммируются. Поскольку частоты колебаний имеют хоть и небольшие, но отличия, через некоторое время колебания войдут в противофазу. В этот момент суммарная амплитуда станет равна нулю: колебания взаимно «погасятся». К моменту времени колебания вновь окажутся в фазе и т. д. (рисунок ).
Период биений – это минимальное значение интервала между двумя моментами времени, которым соответствуют максимальная и минимальная амплитуда колебаний.
Формула, которая определяет медленно изменяющуюся амплитуду результирующего колебания, имеет запись:
.
Период изменения амплитуды равен . Мы можем это продемонстрировать, приняв следующее предположение: периоды колебаний давлений в звуковых волнах и являются такими, что (т. е. ). За период биений наблюдается некоторое число полных циклов колебаний первой волны и циклов колебаний второй волны:
.
Отсюда следует:
или .
есть частота биений, определяемая как разность частот двух звуковых волн, которые воспринимаются ухом одновременно.
Органы слуха человека способны к восприятию звуковых биений до частот . Прослушивание биений – это важный элемент техники настройки музыкальных инструментов.
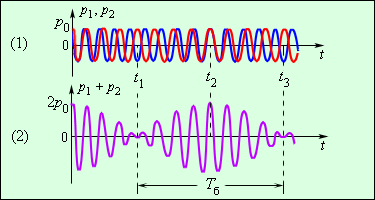
Рисунок Биения, возникающие, когда накладываются две звуковые волны с близкими частотами.
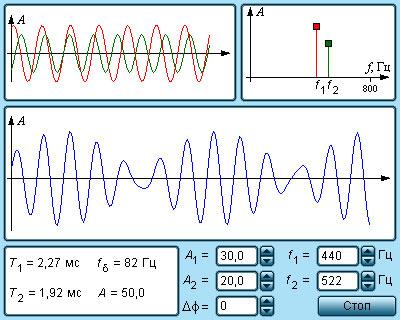
Рисунок Модель явления биений.




