Элементы гидростатики

Перед тем, как приступить к основной части статьи, охарактеризуем жидкость.

Когда тело погружено в жидкость или газ, на него воздействуют силы, распределяемые по поверхности этого тела. И, чтобы описать эти распределенные силы, была введена такая физическая величина, как давление.

Зачастую используют внесистемные единицы: нормальная атмосфера $\left(атм\right)$ и миллиметр ртутного столба $(мм Hg)$: $1 атм=101325 Па=760 мм Hg$.

Закон Паскаля

Французский ученый Б. Паскаль в середине XVII века эмпирическим образом установил закон, который получил название закон Паскаля.

Проиллюстрируем закон Паскаля, изобразив на рисунке $1.15.1.$ небольшую прямоугольную призму, помещенную в жидкость. Предположим, что плотность материала призмы равна плотности жидкости, тогда призма будет находиться в безразличном равновесии с жидкостью. Это значит, что силы давления, воздействующие на грани призмы, должны быть уравновешены, что возможно тогда, когда силы, оказывающие давление на единицу площади поверхности каждой грани, являются одинаковыми: $p_1=p_2=p_3=p$.

Рис. $1.15.1.$ Иллюстрация закона Паскаля.

То, с каким давлением воздействует жидкость на дно или стенки сосуда, имеет зависимость от высоты столба жидкости или глубины. Сосуд цилиндрической формы имеет высоту $h$ и площадь основания $S$, тогда сила давления на дно этого сосуда равна весу столба жидкости $mg$, а, в свою очередь, $m=\rho ghS$, что есть масса жидкости в сосуде ($\rho$ – плотность жидкости). Таким образом, $p=\frac{\rho hSg}{S}=\rho gh$.

Аналогичное давление на глубине $h$, согласно закону Паскаля, окажет жидкость и на стенки сосуда.

Теперь представим, что жидкость помещена в цилиндр с поршнем площадью $S$. Окажем на поршень внешнюю силу $\overrightarrow{F}$, что позволит создать в жидкости дополнительное давление $p_0=\frac{F}{S}$ (рисунок $1.15.2$).

Полное давление в жидкости на глубине $h$ запишем как: $p=p_0+\rho gh$.

Уберем поршень, и тогда давление на поверхность жидкости станет равным атмосферному давлению: $p_0=p_{атм}$.

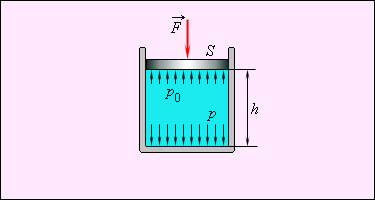
Рис. $1.15.2.$ Зависимость давления от высоты столба жидкости.

Закон Архимеда

Вследствие разности давлений в жидкости на разных уровнях появляется архимедова сила F_formula__А или сила выталкивающая.

Возникновение выталкивающей силы поясним на рисунке $1.15.3.$

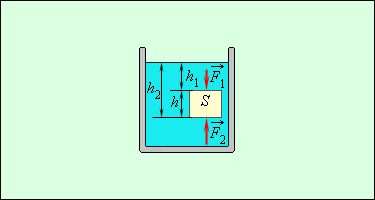
Рис. $1.15.3.$ Архимедова сила. $F_{А}=F_2–F_1=S(p_2–p_1)=\rho gSh, F_1=p_{1}S, F_2=p_{2}S$.

Прямоугольный параллелепипед ($h$ – высота, $S$ – площадь основания) погрузим в жидкость. Запишем разность давлений на нижнюю и верхнюю грани: $\Delta p=p_2–p_1=\rho gh$. Таким образом, выталкивающая сила $F_{А}$ будет иметь направление вверх, и ее модуль: $F_{А}=F_2 – F_1=S\Delta p=\rho gSh=\rho gV$ ($V$ является объемом вытесненной жидкости; $\rho V$– ее массой).

Закон Архимеда применим к телам любой формы.

Следствием из закона Архимеда является утверждение, что, если средняя плотность тела ${\rho }_{т}$ больше плотности жидкости (или газа) $\rho$, тело опустится на дно. Если же ${\rho }_{т}<\rho$, тело будет плавать на поверхности жидкости. Объем той части тела, которая погружена в жидкость, будет таким, что вес вытесненной жидкости станет равным весу тела. Чтобы поднять воздушный шар в воздух, его вес должен быть меньше, чем вес вытесненного воздуха. Именно по этой причине воздушные шары наполняют легкими газами (водородом, гелием) либо нагретым воздухом.

Мы получили выше формулу, определяющую полное давление в жидкости $p=p_0+\rho gh$; из нее следует, что в сообщающихся сосудах любой формы, наполненных однородной жидкостью, давления в любой точке на одном и том же уровне одинаковы (рис. $1.15.4$).

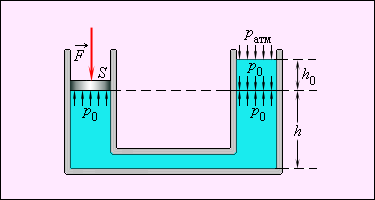
Рис. $1.15.4.$ Пример сообщающихся сосудов. В правом сосуде поверхность жидкости свободна. На уровне $h$ давление в обоих сосудах одинаково $и$ равно $p_0=\frac{F}{S}=\rho g{h}_0+p_{атм}$. Давление на дно сосудов $p=p_0+\rho gh$.

Закрыв поршнями оба цилиндра вертикального расположения сообщающихся сосудов и приложив внешнюю силу к поршням, мы создадим в жидкости большое давление $p$, во много раз превышающее гидростатическое давление $\rho gh$ в любой точке системы. В таком случае можно утверждать, что во всей системе установлено одинаковое давление $p$.

При разных площадях поршней ($S_1$ и $S_2$) и воздействие на них силы со стороны жидкости будет разным ($F_1=p{S}_1$ и $F_2=p{S}_2$). Для удержания системы в состоянии равновесия прикладываемые силы к поршням должны быть такими же по модулю, но имеющими противоположную направленность. В итоге имеем: $\frac{F_1}{S_1}=\frac{F_2}{S_2}$ или $F_2=F_1\frac{S_2}{S_1}$.

Если $S_2\gg S_1$, то $F_2\gg F_1$. Устройства такого строения дают возможность использовать значительный выигрыш в силе и называются гидравлическими машинами (рис. $1.15.5$). При перемещении поршня в узком цилиндре вниз под воздействием внешней силы $F_1$ на расстояние $h_1$ поршень в широком цилиндре сдвинется на расстояние $h_2=\frac{S_1}{S_2}{h}_1$, поднимая тяжелый груз.

Из всего сказанного следует:

Данное правило справедливо для всех идеальных машин, в которых исключена сила трения.

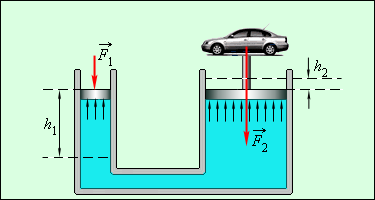
Рис. $1.15.5.$ Гидравлическая машина.

Домкраты широко применяются, в том числе, в качестве гидравлических прессов. В качестве жидкости обычно используют минеральные масла.