Закон сохранения импульса. Реактивное движение

Содержание:

22 сентября 2023
6 минут
3578

Преподаватель физики

Закон сохранения импульса

Закон сохранения импульса можно наблюдать повсюду. Он достаточно точно выполняется в реальных условиях, если пренебречь сопротивлением воздуха, силами трения и т.д. Примеры проявления этого закона:

стрелок ощущает отдачу при выстреле из ружья;
рыбак переходит с кормы на нос лодки, а лодка при этом движется в противоположную сторону;
шары сталкиваются на бильярдном столе.

Однако, прежде чем говорить о законе сохранении импульса, рассмотрим понятие замкнутой системы.

Замкнутая система - система тел, на которую со стороны других тел не действуют внешние силы.

Формулировка закона сохранения импульса (ЗСИ)

Векторная сумма импульсов всех тел, входящих в замкнутую систему, остается постоянной при любых взаимодействиях этих тел между собой внутри системы.

Данный закон является следствием из второго и третьего законов Ньютона. Покажем это.

Возьмем замкнутую систему из двух взаимодействующих тел. Силы $\vec{F_{1}}$ и $\vec{F_{2}}$ - это силы взаимодействия между телами. Третий закон Ньютона гласит, что $\vec{F_{2}} = - \vec{F_{1}}$ . Пусть тела взаимодействуют во течение времени $t$ . Тогда импульсы сил одинаковы по модулю и противоположны по направлению, как и сами силы.

$\vec{F_{2} t} = - \vec{F_{1}} t$ .

По второму закону Ньютона:

$\vec{F_{1}} t = m_{1} \vec{{v_{1}}^{'}} - m_{1} \vec{v_{1}}; \vec{F_{2}} t = m_{1} \vec{{v_{2}}^{'}} - m_{1} \vec{v_{2}}$

Здесь $\vec{{v_{1}}^{'}}$ и $\vec{{v_{2}}^{'}}$ - скорости тел в конце взаимодействия. Соответственно, скорости без штрихов обозначают эти величины в начальный момент взаимодействия.

Из записанного выше следует соотношение:

$m_{1} \vec{v_{1}} + m_{2} \vec{v_{2}} = m_{1} \vec{{v_{1}}^{'}} + m_{2} \vec{{v_{2}}^{'}}$

Это равенство - математическая форма записи закона сохранения импульса. Оно означает, что суммарный импульс системы в результате какого-то взаимодействия не изменился.

Проиллюстрируем закон сохранения импульса на примере соударения шаров разных масс. Один из шаров до удара покоился.

Закон сохранения импульса

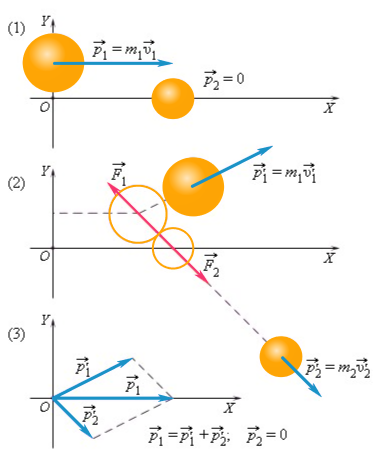
Как видим, после удара векторная сумма импульсов двух шаров равна первоначальному импульсу движущегося шара.

Важно! Закон сохранения выполняется и для проекций векторов на координатные оси.

Закон сохранения импульса позволяет решать задачи и находить скорости тел не зная значений действующих сил.

Рассмотрим снаряд, вылетающий из пушки.

Закон сохранения импульса

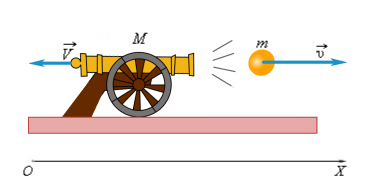
В данном случае взаимодействующие тела - это снаряд и пушка. Сначала тела не движутся. При выстреле снаряд приобретает скорость $\vec{v}$ и летит вперед, а пушка откатывается назад со скоростью $\vec{V}$ . Откатывание пушки называется отдачей от выстрела.

По закону сохранения импульса в проекции на ось OX можно записать:

$m v - M V = 0$

$V = \frac{m v}{M}$ .

Реактивное движение

Реактивное движение также основано на принципе отдачи. Нагретые газы выбрасываются из сопла реактивного двигателя со скоростью $\vec{u}$ . Пусть масса газов равна $m$ , а масса ракеты после истечения газов - $M$ . Рассматривая замкнутую систему "ракета-газы" и применяя к ней закон сохранения импульса, можно вычислить скорость ракеты $V$ после истечения газов.

$V = \frac{m u}{M}$

Формула для пушки и снаряда не применима к ракете, так как дает лишь приблизительное представление о движении ракеты, На самом деле вся масса газов выходит из сопла не сразу, а постепенно.

Рассмотрим этот процесс подробнее. Пусть масса ракеты в момент времени $t$ равна $M$ , а сама ракета движется со скоростью $\vec{v}$ . В течение малого промежутка времени $∆ t$ из сопла ракеты выбрасывается порция газа с относительной скоростью $\vec{u}$ . По истечении времени $∆ t$ ракета будет двигаться со скоростью $v + ∆ v$ , а масса ракеты станет равной $M - ∆ M$ .

В момент $t + ∆ t$ импульс ракеты равен:

$(M - ∆ M) \cdot (\vec{v} + ∆ \vec{v})$ .

Импульс реактивных газов:

$∆ M \cdot (\vec{v} + \vec{u})$ .

По закону сохранения импульса:

$M \vec{v} = (M - ∆ M) \cdot (\vec{v} + ∆ \vec{v}) + ∆ M \cdot (\vec{v} + \vec{u})$ .

Или

$M \vec{∆ v} = ∆ M \cdot \vec{u} - ∆ M \cdot ∆ \vec{v}$ .

Реактивное движение

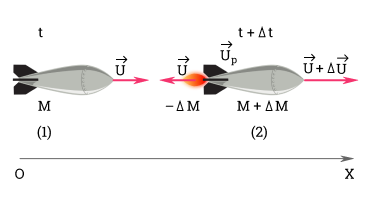
Величиной $∆ M \cdot ∆ \vec{v}$ можно пренебречь, так как $∆ M$ намного меньше $M$ .

Разделим последнее равенство на $∆ t$ и перейдем к пределу $∆ t \to 0$ .

$M \frac{\vec{∆ v}}{∆ t} = ∆ M \cdot \frac{\vec{u}}{∆ t} (∆ t \to 0)$

$M \vec{a} = - μ \vec{u}$ .

Здесь $μ$ - расход топлива в единицу времени, а $- μ \vec{u}$ - реактивная сила тяги. Направление этой силы совпадает с направлением движения ракеты.

Формула $M \vec{a} = - μ \vec{u}$ выражает второй закон Ньютона для тела переменной массы. В скалярном виде ее можно переписать так:

$M a = μ u$ .

Конечная скорость ракеты определяется по формуле:

$v = u \ln (\frac{M_{0}}{M})$ .

Это так называемая формула Циолковского, согласно которой конечная скорость ракеты может превышать скорость истечения газов из сопла двигателя. Правда, достижение такой скорости связано с определенными сложностями. Во-первых, такими, как значительный расход топлива.

Для того, чтобы развить первую космическую скорость $v = v_{1} = 7, 9 \cdot 10^{3} \frac{м}{с}$ при скорости истечения газов $u = 3 \cdot 10^{3} \frac{м}{с}$ стартовая масса ракеты должна быть примерно в 14 раз больше конечной массы.

Современное ракетостроение развивается в направлении экономичных многоступенчатых ракет. Сброс отсеков с отработанным топливом позволяет значительно сократить массу ракеты и оптимизировать дальнейший расход топлива для ее разгона.