
Статью подготовили специалисты образовательного сервиса Zaochnik.
Деление натуральных чисел с остатком: правило, примеры решений
Содержание:
Многие числа нельзя разделить нацело, при делении часто присутствует остаток, отличный от нуля. В этой статье мы разберем способы деления натуральных чисел с остатком и подробно рассмотрим их применение на примерах.
Начнем с деления натуральных чисел с остатком в столбик, затем рассмотрим деление с помощью последовательного вычитания. Наконец, закончим разбором метода подбора неполного частного. Приведем алгоритм деления с остатком для наиболее общего случая и покажем, как проводить проверку результата деления натуральных чисел с остатком.
Деление натуральных чисел столбиком с остатком
Это один из самых удобных способов деления. Подробно он описан в отдельной статье, посвященной делению натуральных чисел столбиком. Здесь мы не будем приводить всю теорию заново, но сконцентрируемся именно на случае деления с остатком.
Приведем решение примера, так как понять суть метода проще всего на практике.
Разделим натуральное число на натуральное число .
Проводим деление столбиком и записываем:
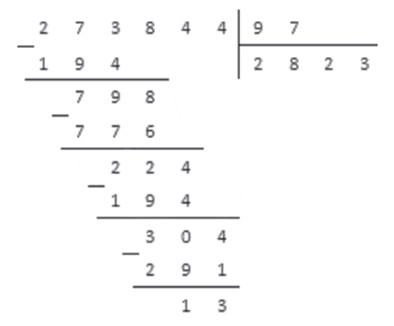
Результат: неполное частное от деления равно , а остаток равен .
Деление чисел с остатком через последовательное вычитание
Чтобы найти неполное частное и остаток, можно прибегнуть к последовательному вычитанию делителя из делимого. Этот способ не всегда целесообразен, однако в некоторых случаях его очень удобно применять. Вновь обратимся к примеру.
Пусть у нас есть яблок. Нам нужно эти яблок разложить в пакеты по яблока. Иными словами, разделить на .
Возьмем из начального количества яблок штуки и положим в один пакет. У нас останется яблока. Теперь, из оставшихся яблок снова отнимаем штуки и кладем уже в другой пакет. Остается яблоко.
яблоко - это остаток от деления, так как на этом этапе мы уже не можем сформировать еще один пакет с тремя яблоками и деление, по сути, завершено. Результат деления:
Это значит, что число как бы умещается в числе два раза, а единица - остаток, меньший чем .
Рассмотрим еще один пример. На этот раз, приведем только математические выкладки, не прибегая к аналогиям.
Вычислим: .
.
Число больше, чем , поэтому продолжаем последовательное вычитание делителя:
.
Повторяем эту операцию еще раз:
В результате, нам понадобилось последовательно вычесть делитель из делимого раза до того, как мы получили остаток - результат вычитания, который меньше делителя. В нашем случае остатком является число .
.
Метод последовательного вычитания непригоден, когда делимое меньше делителя. В таком случае можно сразу записать ответ: неполное частное равно нулю, а остаток равен самому делимому.
Если , то .
Например:
Также касательно метода последовательного вычитания нужно отметить, что он удобен только в случаях, когда вся операция деления сводится к небольшому количеству вычитаний. Если делимое во много раз больше делителя, использование этого метода будет нецелесообразно и связано с множеством громоздких вычислений.
Метод подбора неполного частного
При делении натуральных чисел с остатком можно вычислить результат методом подбора неполного частного. Покажем, как можно вести процесс подбора, и на чем он основан.
Во-первых, определим, среди каких чисел нужно искать неполное частное. Из самого определения процесса деления понятно, что неполное частное равно нулю, либо является одним из натуральных чисел и т.д.
Во-вторых, установим связь между делителем, делимым, неполным частным и остатком. Рассмотрим уравнение . Здесь - остаток от деления, - делимое, - делитель, - неполное частное.
В-третьих, не будем забывать, что остаток всегда меньше делителя.
Теперь рассмотрим непосредственно процесс подбора. Делимое и делитель известны нам с самого начала. В качестве неполного частного будем последовательно принимать числа из ряда и т.д. Применяя формулу и вычисляя полученное значение с делителем, закончим процесс, когда остаток будет меньше, чем делитель . Число, взятое за на этом шаге и будет неполным частным.
Разберем применение этого метода на примере.
Разделим на .
Подберем неполное частное.
Используем формулу и будем последовательно перебирать , придавая ему значения и т.д.
Если , имеем: . Число больше, чем , поэтому продолжаем подстановку.
При имеем: . Т.к. , снова повторяем процесс.
При имеем: .
При имеем: .
...
При имеем: .
На этом этапе процесс деления можно считать законченным. Неполное частное , а остаток деления равен .
Алгоритм деления натуральных чисел с остатком
Когда рассмотренные выше методы подбора неполного частного и последовательного вычитания требуют слишком громоздких вычислений, для деления с остатком применяется следующий метод. Рассмотрим алгоритм деления натурального числа на число с остатком.
Вспомним, что в случае, когда неполное частное равно нулю, а остаток равен делимомому . Мы будем рассматривать случай, когда .
Сформулируем три вопроса и ответим на них:
- Что там известно?
- Что нам нужно найти?
- Как мы будем это делать?
Изначально известными являются делимое и делитель: и .
Найти нужно неполное частное и остаток .
Приведем формулу, которая задает связь между делимым, делителем, неполным частным и остатком. . Именно это соотношение мы и возьмем за основу алгоритма деления натуральных чисел с остатком. Делимое нужно представить в виде суммы , тогда мы найдем искомые величины.
Алгоритм деления, благодаря которому мы представим в виде суммы очень схож с алгоритмом деления натуральных чисел без остатка. Приведем ниже шаги алгоритма на примере деления числа на .
1. Первым делом смотрим на делимое и делитель. Выясняем и запоминаем, на сколько знаков число в записи делимого больше числа в делителе. В нашем конкретном примере в делимом три знака, а в делителе - два.
Запомним это число.
2. Справа в записи делителя допишем число нулей, определенное разницей между количеством знаков в делимом и делителе. В нашем случае нужно дописать один нуль. Если записанное число больше делимого, то нужно из запомненного в первом пункте числа вычесть единицу.
В нашем примере справа от дописываем нуль. Так как , запомненное в предыдущем пункте число не нужно уменьшать на единицу. Таким образом, число так и остается у нас в памяти.
3. Справа к цифре приписываем количество нулей, равное числу, определенному в предыдущем пункте. В нашем примере, приписывая к единице один нуль, получаем число . В результате данного действия мы получили рабочую единицу разряда, с которым будем работать дальше.
4. Будем последовательно умножать делитель на и т.д. единицы рабочего разряда, пока не получим число, которое больше или равно делимому.
Рабочий разряд в нашем примере - десятки. После умножения делителя на одну единицу рабочего разряда, получаем .
, поэтому умножаем на еще одну единицу рабочего разряда. Получаем: .
Число, которое мы получили на предпоследнем шаге является первым из искомых слагаемых.
5. Найдем разность между делимым и первым найденным слагаемым. Если полученное число больше делителя, то переходим к нахождению второго слагаемого.
Шаги повторяем, однако в качестве делимого принимаем полученное здесь число. Если снова получаем число, большее, чем делитель, снова по-кругу повторяем пункты , но уже с новым числом в качестве делимого. Продолжаем, пока полученное здесь число не будет меньше делителя. Переходим к завершающему этапу. Забегая вперед, скажем, что последнее полученное число и будет равно остатку.
Обратимся к примеру. . Повторяем шаги алгоритма с числом , взятым в качестве делимого.
1. В записи числа на один знак больше, чем в записи числа . Запоминаем разницу - число .
2. В записи делимого справа дописываем один нуль. Получаем число . Так как , из запомненного в предыдущем пункте числа вычитаем и получаем . Запоминаем .
3. Так как в предыдущем пункте мы получили число и запомнили его, нам не нужно прибавлять ни одного нуля к единице справа. Таким образом, рабочим разрядом являются единицы
4. Последовательно умножим делитель на и т.д. Не будем приводить подробные выкладки, а обратим внимание на конечный результат: , . Таким образом, второе искомое слагаемое - .
5. Разность между и равна числу . Так как , это третье, и последнее искомое слагаемое. Перейдем к завершающему этапу алгоритма деления столбиком.
6. Целью предыдущих действий было представление делимого в виде суммы нескольких слагаемых. Для нашего примера мы получили . Вспоминаем, что . Перепишем равенство:
Применим распределительное свойство умножения.
.
Таким образом, мы представили делимое в виде уже данной ранее формулы .
Искомые неизвестные:неполное частное , остаток .
Безусловно, при решении практических примеров нет нужды расписывать все действия так подробно. Покажем это:
Разделим числа и .
Используем алгоритм. Первые пять шагов дают первое слагаемое - число .
Снова повторяем первые пять шагов алгоритма с числом и получаем второе слагаемое
Третий раз проходим шаги аглоритма, но у же с новым числом . Третье слагаемое равно . Остаток равен .
В результате получаем:
Неполное частное равно , остаток равен .
Деление натуральных чисел с остатком. Проверка результата
Деление натуральных чисел с остатком, особенно при больших числах, довольно трудоемкий и громоздкий процесс. Допустить ошибку в вычислениях может каждый. Именно поэтому, проверка результата деления поможет понять, все ли вы сделали правильно. Проверка результата деления натуральных чисел с остатком выполняется в два этапа.
На первом этапе проверяем, не получился ли остаток больше делителя. Если нет, то все хорошо. Иначе, можно сделать вывод, что что-то пошло не так.
Остаток всегда меньше делителя!
На втором этапе проверяется справедливость равенства . Если равенство после подстановки значений оказывается верным, то и деление было выполнено без ошибок.
Проверим, верно ли, что .
Сравниваем остаток и делитель: .
Значит, деление выполнено неверно.
Школьник разделил на и получил в результате неполное частное с остатком . Правильно ли он сделал?
Чтобы узнать это, сначала сравниваем остаток и делитель: .
Первый пункт проверки пройден, переходим ко второму.
Запишем формулу . .
Подставляем значения и сравниваем результаты
Значит, в вычисления школьника где-то закралась ошибка.
Студент выполнял лабораторную работу по физике. В ходе выполнения ему понадобилось разделить на . В результате у него получилось число с остатком . Все ли правильно посчитано?
Проверим! Остаток меньше, чем делитель , поэтому переходим ко второму этапу проверки.
Используем формулу , где .
После подстановки, имеем:
.
Равенство корректно, а значит, и деление выполнено верно.
Навигация по статьям
