Перпендикулярные плоскости, условие перпендикулярности плоскостей

Содержание:

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Данная статья посвящена перпендикулярным плоскостям. Будут даны определения, обозначения вместе с примерами. Будет сформулирован признак перпендикулярности плоскостей и условие, при котором он выполним. Будут рассмотрены решения подобных задач на примерах.

Перпендикулярные плоскости – основные сведения

При наличии угла между пересекающимися прямыми можно говорить об определении перпендикулярных плоскостей.

Определение 1

При условии, что угол между перпендикулярными прямыми равен $90$ градусов, их называют перпендикулярными.

Обозначение перпендикулярности принято писать знаком « $⊥$ ». Если в условии дано, что плоскости $α$ и $β$ перпендикулярные, тогда запись принимает вид $α ⊥ β$ . На рисунке ниже показано подробно.

Перпендикулярные плоскости – основные сведения

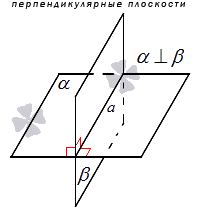
Когда в улови дано, что плоскость $α$ и $β$ перпендикулярны, это значит, что $α$ перпендикулярна $β$ и наоборот. Такие плоскости называют взаимно перпендикулярными. Например, стена и потолок в комнате являются взаимно перпендикулярными, так как при пересечении дают прямой угол.

Перпендикулярность плоскостей – признак и условие перпендикулярности

На практике можно встретить задания, где необходимо определить перпендикулярность заданных плоскостей. Для начала нужно определить угол между ними. Если он равен $90$ градусам, тогда они считаются перпендикулярными из определения.

Для доказательства перпендикулярности двух плоскостей применяют признак перпендикулярности двух плоскостей. Формулировка содержит понятия перпендикулярная прямая и плоскость. Напишем точное определение признака перпендикулярности в виде теоремы.

Теорема 1

Если одна из двух заданных плоскостей пересекает прямую, перпендикулярную другой плоскости, то заданные плоскости перпендикулярны.

Доказательство имеется в учебнике по геометрии за $10 - 11$ класс, где есть подробное описание. Из признака следует, что, если плоскость перпендикулярна линии пересечения двух заданных плоскостей, то она перпендикулярна к каждой из этих плоскостей.

Существует необходимое и достаточное условия для доказательства. Рассмотрим их для перпендикулярности двух заданных плоскостей, которое применяется в качестве проверки их перпендикулярности, находящихся в прямоугольной системе координат трехмерного пространства. Чтобы доказательство имело силу, необходимо применить определение нормального вектора плоскости, который способствует доказать необходимое и достаточное условие перпендикулярности плоскостей.

Теорема 2

Для того, чтобы перпендикулярность пересекающихся плоскостей была явной, необходимо и достаточно, чтобы нормальные векторы заданных плоскостей пересекались под прямым углом.

Доказательство

Пусть в трехмерном пространстве задана прямоугольная система координат. Если имеем $\vec{n_{1}} = (A_{1}, B_{1}, C_{1})$ и $\vec{n_{2}} = (A_{2}, B_{2}, C_{2})$ , являющимися нормальными векторами заданных плоскостей $α$ и $β$ , то необходимым и достаточным условием перпендикулярности векторов $\vec{n_{1}}$ и $\vec{n_{2}}$ примет вид

$(\vec{n_{1}}, \vec{n_{2}}) = 0 \Leftrightarrow A_{1} \cdot A_{2} + B_{1} \cdot B_{2} + C_{1} \cdot C_{2} = 0$

Отсюда получаем, что $\vec{n_{1}} = (A_{1}, B_{1}, C_{1})$ и $\vec{n_{2}} = (A_{2}, B_{2}, C_{2})$ - нормальные векторы заданных плоскостей, а для действительности перпендикулярности $α$ и $β$ необходимо и достаточно, чтобы скалярное произведение векторов $\vec{n_{1}}$ и $\vec{n_{2}}$ было равным нулю, а значит, принимало вид $(\vec{n_{1}}, \vec{n_{2}}) = 0 \Leftrightarrow A_{1} \cdot A_{2} + B_{1} \cdot B_{2} + C_{1} \cdot C_{2} = 0$ .

Равенство выполнено.

Рассмотрим подробнее на примерах.

Пример 1

Определить перпендикулярность плоскостей, заданных в прямоугольной системе координат $O x y z$ трехмерно пространства, заданного уравнениями $x - 3 y - 4 = 0$ и $\frac{x}{\frac{2}{3}} + \frac{y}{- 2} + \frac{z}{\frac{4}{5}} = 1$ ?

Решение

Для нахождения ответа на вопрос о перпендикулярности для начал необходимо найти координаты нормальных векторов заданных плоскостей, после чего можно будет выполнить проверку на перпендикулярность.

$x - 3 y - 4 = 0$ является общим уравнением плоскости, из которого можно сразу преобразовать координаты нормального вектора, равные $\vec{n_{1}} = (1, - 3, 0)$ .

Для определения координаты нормального вектора плоскости $\frac{x}{\frac{2}{3}} + \frac{y}{- 2} + \frac{z}{\frac{4}{5}} = 1$ перейдем от уравнения плоскости в отрезках к общему.

Тогда получим:

$\frac{x}{\frac{2}{3}} + \frac{y}{- 2} + \frac{z}{\frac{4}{5}} \Leftrightarrow \frac{3}{2} x - \frac{1}{2} y + \frac{5}{4} z - 1 = 0$

Тогда $\vec{n_{2}} = (\frac{3}{2}, - \frac{1}{2}, \frac{5}{4})$ - это координаты нормального вектора плоскости $\frac{x}{\frac{2}{3}} + \frac{y}{- 2} + \frac{z}{\frac{4}{5}} = 1$ .

Перейдем к вычислению скалярного произведения векторов $\vec{n_{1}} = (1, - 3, 0)$ и $\vec{n_{2}} = (\frac{3}{2}, - \frac{1}{2}, \frac{5}{4})$ .

Получим, что $(\vec{n_{1}}, \vec{n_{2}}) = 1 \cdot \frac{3}{2} + (- 3) \cdot (- \frac{1}{2}) + 0 \cdot \frac{5}{4} = 3$ .

Видим, что оно не равно нулю, значит, что заданные векторы не перпендикулярны. Отсюда следует, что плоскости также не перпендикулярны. Условие не выполнено.

Ответ: плоскости не перпендикулярны.

Пример 2

Прямоугольная система координат $O x y z$ имеет четыре точки с координатами $A (- \frac{15}{4}, - \frac{7}{8}, 1), B (\frac{17}{8}, \frac{5}{16}, 0), C (0, 0, \frac{3}{7}), D (- 1, 0, 0)$ . Проверить, перпендикулярны ли плоскости $А В С$ и $A B D$ .

Решение

Для начала необходимо рассчитать скалярное произведение векторов данных плоскостей. Если оно равно нулю, только в этом случае можно считать, что они перпендикулярны. Находим координаты нормальных векторов $\vec{n_{1}}$ и $\vec{n_{2}}$ плоскостей $А В С$ и $A B D$ .

Из заданных координат точек вычислим координаты векторов $\vec{A B}, \vec{A C}, \vec{A D}$ . Получаем, что:

$\vec{A B} = (\frac{47}{8}, \frac{19}{16}, - 1), \vec{A C} = (\frac{15}{4}, \frac{7}{8}, - \frac{4}{7}), \vec{A D} = (\frac{11}{4}, \frac{7}{8}, - 1)$ .

Нормальный вектор плоскости $А В С$ является векторным произведением векторов $\vec{A B}$ и $\vec{A C}$ , а для $A B D$ векторное произведение $\vec{A B}$ и $\vec{A D}$ . Отсюда получим, что

$\vec{n_{1}} = [\vec{A B} \times \vec{A C}] = |\begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ \frac{47}{8} & \frac{19}{16} & - 1 \\ \frac{15}{4} & \frac{7}{8} & - \frac{4}{7} \end{matrix}| = \frac{11}{56} \cdot \vec{i} - \frac{11}{28} \cdot \vec{j} + \frac{11}{16} \cdot \vec{k} \Leftrightarrow \vec{n_{1}} = (\frac{11}{56}, - \frac{11}{28}, \frac{11}{16}) \vec{n_{2}} = [\vec{A B} \times \vec{A D}] = |\begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ \frac{47}{8} & \frac{19}{16} & - 1 \\ \frac{11}{4} & \frac{7}{8} & - 1 \end{matrix}| = - \frac{5}{16} \cdot \vec{i} + \frac{25}{8} \cdot \vec{j} + \frac{15}{8} \cdot \vec{k} \Leftrightarrow \vec{n_{2}} = (- \frac{5}{16}, \frac{25}{8}, \frac{15}{8})$

Приступим к нахождению скалярного произведения $\vec{n_{1}} = (\frac{11}{56}, - \frac{11}{28}, \frac{11}{16})$ и $\vec{n_{2}} = (- \frac{5}{16}, \frac{25}{8}, \frac{15}{8})$ .

Получим: $(\vec{n_{1}}, \vec{n_{2}}) = \frac{11}{56} \cdot (- \frac{5}{16}) + (- \frac{11}{28}) \cdot \frac{25}{8} + \frac{11}{16} \cdot \frac{15}{8} = 0$ .

Если оно равно нулю, значит векторы плоскостей $А В С$ и $A B D$ перпендикулярны, тогда и сами плоскости перпендикулярны.

Ответ: плоскости перпендикулярны.

Можно было подойти к решению иначе и задействовать уравнения плоскостей $А В С$ и $A B D$ . После нахождения координат нормальных векторов данных плоскостей можно было бы проверить на выполнимость условие перпендикулярности нормальных векторов плоскостей.

Курсовая работа по математике

от 5 дней/ от 2160 р.

Реферат по математике

от 1 дня/ от 840 р.

Решение задач по математике

от 1 дня/ от 150 р.