Емкость конденсаторов: определение, формулы, примеры.

Определение 1

Конденсатор – это совокупность двух любых проводников, заряды которых одинаковы по значению и противоположны по знаку.

Его конфигурация говорит о том, что поле, созданное зарядами, локализовано между обкладками. Тогда можно записать формулу электроемкости конденсатора:

$C = \frac{q}{φ_{1} - φ_{2}} = \frac{q}{U}$ $C = \frac{q}{φ_{1} - φ_{2}} = \frac{q}{U}$ .

Значением $φ_{1} - φ_{2} = U$ $φ_{1} - φ_{2} = U$ обозначают разность потенциалов, называемую напряжением, то есть $U$ $U$ . По определению емкость положительна. Она зависит только от размерностей обкладок конденсатора их взаиморасположения и диэлектрика. Ее форма и место должны минимизировать воздействие внешнего поля на внутреннее. Силовые линии конденсатора начинаются на проводнике с положительным зарядом, а заканчиваются с отрицательным. Конденсатор может являться проводником, помещенным в полость, окруженным замкнутой оболочкой.

Выделяют три большие группы: плоские, сферические, цилиндрические. Чтобы найти емкость, необходимо обратиться к определению напряжения конденсатора с известными значениями зарядов на обкладках.

Плоский конденсатор

Определение 2

Плоский конденсатор – это две противоположно заряженные пластины, которые разделены тонким слоем диэлектрика, как показано на рисунке $1$ $1$ .

Формула для расчета электроемкости записывается как

$C = \frac{ε ε_{0} S}{d}$ $C = \frac{ε ε_{0} S}{d}$ , где $S$ $S$ является площадью обкладки, $d$ $d$ – расстоянием между ними, $ε$ $ε$ - диэлектрической проницаемостью вещества. Меньшее значение $d$ $d$ способствует большему совпадению расчетной емкости конденсатора с реальной.

Плоский конденсатор

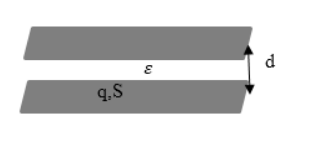
Рисунок $1$ $1$

При известной электроемкости конденсатора, заполненного $N$ $N$ слоями диэлектрика, толщина слоя с номером $i$ $i$ равняется $d_{i}$ $d_{i}$ , вычисление диэлектрической проницаемости этого слоя $ε_{i}$ $ε_{i}$ выполняется, исходя из формулы:

$C = \frac{ε_{0} S}{\frac{d_{1}}{ε_{1}} + \frac{d_{2}}{ε_{2}} + . . . + \frac{d_{N}}{ε_{N}}}$ $C = \frac{ε_{0} S}{\frac{d_{1}}{ε_{1}} + \frac{d_{2}}{ε_{2}} + . . . + \frac{d_{N}}{ε_{N}}}$ .

Сферический конденсатор

Определение 3

Когда проводник имеет форму шара или сферы, тогда внешняя замкнутая оболочка является концентрической сферой, это означает, что конденсатор сферический.

Он состоит из двух концентрических проводящих сферических поверхностей с пространством между обкладками, заполненным диэлектриком, как показано на рисунке $2$ $2$ . Емкость рассчитывается по формуле:

$C = 4 π ε ε_{0} \frac{R_{1} R_{2}}{R_{2} - R_{1}}$ $C = 4 π ε ε_{0} \frac{R_{1} R_{2}}{R_{2} - R_{1}}$ , где $R_{1}$ $R_{1}$ и $R_{2}$ $R_{2}$ являются радиусами обкладок.

Сферический конденсатор

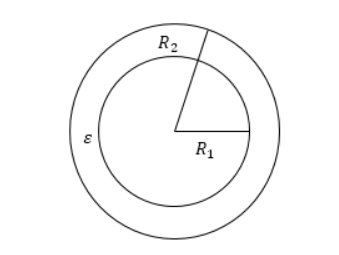
Рисунок $2$ $2$

Цилиндрический конденсатор

Емкость цилиндрического конденсатора равняется:

$C = \frac{2 {πεε}_{0} l}{\ln (\frac{R_{2}}{R_{1}})}$ $C = \frac{2 {πεε}_{0} l}{\ln (\frac{R_{2}}{R_{1}})}$ , где $l$ $l$ - высота цилиндров, $R_{1}$ $R_{1}$ и $R_{2}$ $R_{2}$ - радиусы обкладок. Данный вид конденсатора имеет две соосные поверхности проводящих цилиндрических поверхности, как показано на рисунке $3$ $3$ .

Цилиндрический конденсатор

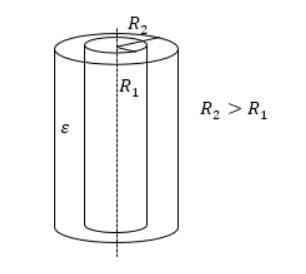
Рисунок $3$ $3$

Определение 4

Важной характеристикой конденсаторов считается пробивное напряжение - напряжение, при котором происходит электрический разряд через слой диэлектрика.

$U_{m a x}$ $U_{m a x}$ находится от зависимости от толщины слоя и свойств диэлектрика, конфигурации конденсатора.

Электроемкость плоского конденсатора. Формулы

Кроме отдельных конденсаторов используются их соединения. Наличие параллельного соединения конденсаторов применяют для увеличения его емкости. Тогда поиск результирующей емкости соединения сводится к записи суммы $C_{i}$ $C_{i}$ , где $C_{i}$ $C_{i}$ - это емкость конденсатора с номером $i$ $i$ :

$C = \sum_{i = 1}^{N} C_{i}$ $C = \sum_{i = 1}^{N} C_{i}$ .

При последовательном соединении конденсаторов суммарная емкость соединения всегда будет по значению меньше, чем минимальная любого конденсатора, входящего в систему. Для расчета результирующей емкости следует сложить величины, обратные к емкостям отдельных конденсаторов:

Пример 1

Произвести вычисление емкости плоского конденсатора при известной площади обкладок
$1 с м^{2}$ $1 с м^{2}$ с расстоянием между ними $1 м м$ $1 м м$ . Пространство между обкладками находится в вакууме.

Решение

Чтобы рассчитать электроемкость конденсатора, применяется формула:

$C = \frac{ε ε_{0} S}{d}$ $C = \frac{ε ε_{0} S}{d}$ .

Значения:

$ε = 1, ε_{0} = 8, 85 \cdot 10^{- 12} \frac{Ф}{м}; S = 1 с м^{2} = 10^{- 4} м^{2}; d = 1 м м = 10^{- 3} м .$ $ε = 1, ε_{0} = 8, 85 \cdot 10^{- 12} \frac{Ф}{м}; S = 1 с м^{2} = 10^{- 4} м^{2}; d = 1 м м = 10^{- 3} м .$

Подставим числовые выражения и вычислим:

$C = \frac{8, 85 \cdot 10^{- 12} \cdot 10^{- 4}}{10^{- 3}} = 8, 85 \cdot 10^{- 13} (Ф)$ $C = \frac{8, 85 \cdot 10^{- 12} \cdot 10^{- 4}}{10^{- 3}} = 8, 85 \cdot 10^{- 13} (Ф)$ .

Ответ: $C \approx 0, 9 п Ф$ $C \approx 0, 9 п Ф$ .

Пример 2

Найти напряженность электростатического поля у сферического конденсатора на расстоянии $x = 1 с м = 10^{- 2} м$ $x = 1 с м = 10^{- 2} м$ от поверхности внутренней обкладки при внутреннем радиусе обкладки, равном $R_{1} = 1 с м = 10^{- 2} м$ $R_{1} = 1 с м = 10^{- 2} м$ , внешнем – $R_{2} = 3 с м = 3 \cdot 10^{- 2} м$ $R_{2} = 3 с м = 3 \cdot 10^{- 2} м$ . Значение напряжения - $10^{3} В$ $10^{3} В$ .

Решение

Производящая заряженная сфера создает напряженность поля. Его значение вычисляется по формуле:

$E = \frac{1}{4 π ε ε_{0}} \frac{q}{r^{2}}$ $E = \frac{1}{4 π ε ε_{0}} \frac{q}{r^{2}}$ , где $q$ $q$ обозначают заряд внутренней сферы, $r = R_{1} + x$ $r = R_{1} + x$ - расстояние от центра сферы.

Нахождение заряда предполагает применение определения емкости конденсатора С:

$q = C U$ $q = C U$ .

Для сферического конденсатора предусмотрена формула вида

$C = 4 π ε ε_{0} \frac{R_{1} R_{2}}{R_{2} - R_{1}}$ $C = 4 π ε ε_{0} \frac{R_{1} R_{2}}{R_{2} - R_{1}}$ с радиусами обкладок $R_{1}$ $R_{1}$ и $R_{2}$ $R_{2}$ .

Производим подстановку выражений для получения искомой напряженности:

$E = \frac{1}{4 {πεε}_{0}} \frac{U}{(x + R_{1})^{2}} 4 {πεε}_{0} \frac{R_{1} R_{2}}{R_{2} - R_{1}} = \frac{U}{(x + R_{1})^{2}} \frac{R_{1} R_{2}}{R_{2} - R_{1}}$ $E = \frac{1}{4 {πεε}_{0}} \frac{U}{(x + R_{1})^{2}} 4 {πεε}_{0} \frac{R_{1} R_{2}}{R_{2} - R_{1}} = \frac{U}{(x + R_{1})^{2}} \frac{R_{1} R_{2}}{R_{2} - R_{1}}$ .

Данные представлены в системе $С И$ $С И$ , поэтому достаточно заменить буквы числовыми выражениями:

$E = \frac{10^{3}}{(1 + 1)^{2} \cdot 10^{- 4}} \cdot \frac{10^{- 2} \cdot 3 \cdot 10^{- 2}}{3 \cdot 10^{- 2} - 10^{- 2}} = \frac{3 \cdot 10^{- 1}}{8 \cdot 10^{- 6}} = 3, 45 \cdot 10^{4} (\frac{В}{м})$ $E = \frac{10^{3}}{(1 + 1)^{2} \cdot 10^{- 4}} \cdot \frac{10^{- 2} \cdot 3 \cdot 10^{- 2}}{3 \cdot 10^{- 2} - 10^{- 2}} = \frac{3 \cdot 10^{- 1}}{8 \cdot 10^{- 6}} = 3, 45 \cdot 10^{4} (\frac{В}{м})$ .

Ответ: $E = 3, 45 \cdot 10^{4} \frac{В}{м}$ $E = 3, 45 \cdot 10^{4} \frac{В}{м}$ .