- 24 июля 2025
- 6 минут
- 9 490
Циркуляция вектора напряженности электростатического поля
Статью подготовили специалисты образовательного сервиса Zaochnik.
Было выявлено, что на заряд , находящийся в электростатическом поле, действуют консервативные силы, причем работа на замкнутом пути равняется нулю:
, где - это вектор перемещения. Данный интеграл представляет собой циркуляцию вектора напряженности электростатического поля.
Если единичный заряд положительный, то запись приобретает совсем другой вид. Интеграл левой части уравнения и является циркуляцией вектора напряженности по контуру .
Теорема о циркуляции
Электростатическое поле характеризуется циркуляцией его вектора напряженности по замкнутому полю и равняется нулю. Утверждение называют теоремой о циркуляции вектора напряженности электростатического поля.
Для ее доказательства основываются на работе поля по перемещению заряда, не зависящую от ее траектории. и обозначают в качестве различных путей между точками и . При замене их местами получим . Теорема доказана
Следствие теоремы о циркуляции. Теорема Стокса
Так как линии на напряженности электростатического поля незамкнуты, то это применяют в качестве следствия. Их начало идет с положительных зарядов, а заканчивается отрицательными или их уходом в бесконечность. Теорема верна для статичных зарядов.
Еще одним следствием является непрерывность тангенциальных составляющих напряженности. Это говорит о том, что ее компоненты, являющиеся касательными к выбранной любой поверхности во всякой точке, на обеих сторонах содержат одинаковые значения.
Необходимо выделить произвольную часть поверхности , которая опирается на контур .
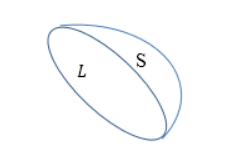
Рисунок
По формуле Стокса интеграл от ротора вектора напряженности , взятый по поверхности
, равняется циркуляции вектора напряженности вдоль контура, на который опирается данная поверхность.
Значение , является единичным вектором, перпендикулярным участку . Интенсивность «завихрения» вектора характеризуется ротором . Это рассматривают на примере наличия крыльчатки, помещенной в жидкости, изображаемой на рисунке . Если ротор не равняется нулю, то крыльчатка будет продолжать вращение, причем с ростом скорости вращения увеличится модуль проекция ротора на ось крыльчатки.
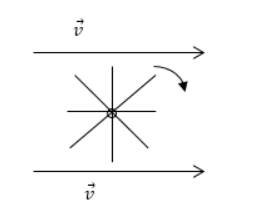
Рисунок
Для вычисления ротора применяют формулы:
Если использовать уравнение , то циркуляция вектора напряженности будет равной нулю.
При выполнении условия для любой поверхности , упирающейся на контур , возможно с подынтегральным выражением, причем для каждой точки поля.
Действие производится аналогично крыльчатке из рисунка . На ее концах имеются одинаковые заряды, равные . Вся система находится в однородном поле с напряженностью . Если , то предусмотрено вращение с ускорением, зависящим от проекции ротора на ось крыльчатки. Если поле электростатическое, тогда движение по окружности не происходило бы ни при каком расположении оси. Основная отличительная особенность электростатического поля в том, что оно является безвихревым.
Представление теоремы о циркуляции в дифференциальном виде:
Дан рисунок с изображением электростатического поля. Что можно сказать о его характеристиках?
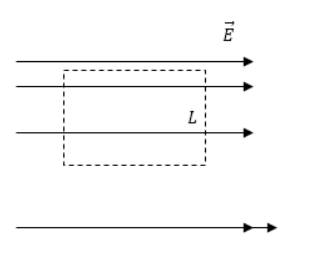
Рисунок
Решение
По рисунку видно, что существование электростатического поля невозможно. Для выделенного пунктиром контура циркуляции вектора напряженности применяется формула:
.
Это невозможно, так как существует противоречие теоремы о циркуляции. Определение напряженности поля (измеряется в вольтах на метр или в ньютонах на кулон ) идет с помощью густоты силовых линий, причем с различными значениями. Работа по замкнутому кругу не равна нулю, значит, циркуляция вектора напряженности также нулю не равняется.
Показать, что тангенциальные составляющие вектора напряженности электростатического поля не изменяются при переходе через границу раздела диэлектриков, основываясь на теореме о циркуляции.
Решение
Если рассмотреть границу между двумя диэлектриками с диэлектрическими проницаемостями и , изображенных на рисунке , то видно, что ось проходит через середины сторон . На границе выбирается прямоугольный контур с параметрами длины и ширины .
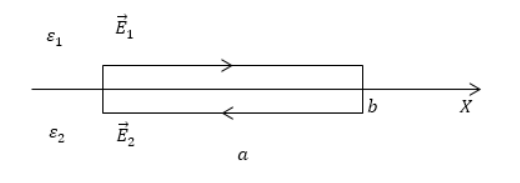
Рисунок
Выполнение теоремы о циркуляции обусловлено наличием электростатического поля. Его находят из формулы:
.
Если контур имеет небольшие размеры, тогда циркуляция вектора напряженности, согласно формуле , представляется в виде:
.
- это среднее значение на участках, перпендикулярных к границе раздела.
Из формулы следует:
.
Когда , тогда
.
Выполнение выражения возможно при произвольном выборе оси , которая располагается на границе раздела диэлектриков. Можно представить вектор напряженности в виде двух: тангенциальной и нормальной :
.
Отсюда следует, что
, где является проекцией вектора напряженности на орт , который направлен вдоль границы раздела диэлектриков.




