- 24 июля 2025
- 10 минут
- 10 328
Закон Био-Савара. Теорема о циркуляции
Статью подготовили специалисты образовательного сервиса Zaochnik.
Французские ученые Ж. Био и Ф. Савар в -м году проводили эксперименты над магнитным полем постоянных токов. Физики доказали, что индукция магнитного поля проходящих по проводнику токов зависит от совместного действия всех участков данного проводника. Работа магнитного поля основана на принципе суперпозиции.
Принцип суперпозиции: если магнитное поле работает за счет нескольких проводников с током, тогда индукция результативного поля – это совокупность индукций полей, которые создаются каждым проводником по отдельности.
Индукция проводника с током представлена, как векторная сумма элементарных индукций вырабатываемых отдельными участками проводника. На практике нельзя отделить один участок проводника с током, поскольку постоянные токи всегда замкнутые. Возможно лишь измерить совокупную индукцию магнитного поля, которое создают все элементы тока. Как найти индукцию магнитного поля?
Закон Био–Савара
Закон Био-Савара определил вклад в магнитную индукцию результативного магнитного поля, образуемый маленьким участком проводника с током .
.
В формуле – это расстояние от заданного участка до точки наблюдения, – это угол между направлением на точку наблюдения и направлением тока на заданном участке, – это магнитная постоянная.
Используя правило буравчика, определим направление вектора : оно указывает на ту сторону, в которую вращается рукоятка буравчика при его поступательном движении вдоль тока. Рисунок наглядно показывает закон Био-Савара с применением магнитного поля прямолинейного проводника с током. Если сложить (интегрировать) вклады в магнитное поле всех участков проводника с током, тогда получим формулу для магнитной индукции поля прямого тока:
.
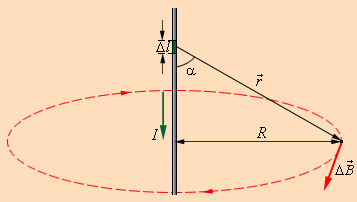
Рисунок Иллюстрация закона Био–Савара.
С помощью этого закона можно определять магнитные поля токов с различными конфигурациями. Запросто рассчитать магнитное поле в центре кругового витка с током. Вычисления приводят к соотношению:
,
где – это радиус кругового проводника.
Чтобы определить направление вектора тоже используется правило буравчика, только в этом случае рукоятка вращается по направлению кругового тока, а поступательное движение буравчика указывает, куда направлен вектор магнитной индукции.
Теорема о циркуляции вектора магнитной индукции
Вычисления магнитного поля зачастую упрощаются с учетом симметрии в конфигурации токов. В этом помогает теорема о циркуляции вектора магнитной индукции.
Объясним, что означает циркуляция вектора . Допустим, в пространстве с магнитным полем существует какой-то условный замкнутый контур, а также положительное направление его обхода. Тогда, на каждом отдельном маленьком участке данного контура определяется касательная составляющая вектора в этом месте, то есть определяется проекция вектора на направление касательной к заданному участку контура. Рисунок наглядно демонстрирует это.
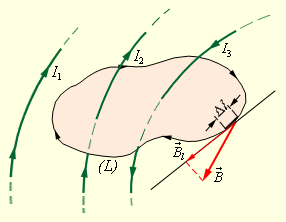
Рисунок Замкнутый контур с заданным направлением обхода. Изображение токов и
, создающих магнитное поле.
Циркуляция вектора – это сумма произведений , взятая по целому контуру :
Некоторые токи, при которых магнитное поле создается, пропускают выбранный контур тем временем, как остальные токи находятся в стороне от контура.
Согласно теореме о циркуляции, циркуляция вектора магнитного поля постоянных токов по любому из контуров все время определяется, как произведение магнитной постоянной на сумму всех токов:
На рисунке продемонстрирован пример с несколькими проводниками с токами, образующими магнитное поле. Ток и ток пронзают контур в противоположных направлениях, им приписываются различные знаки. Положительным является ток, который связан с заданным направлением обхода контура по правилу буравчика.
Значит, , а . Ток не пронзает контур .
Теорема о циркуляции в этом примере математически выражается следующей формулой:
.
Общий вид теоремы о циркуляции можно вывести из принципа суперпозиции и закона Био-Савара.
Самый простой пример использования теоремы о циркуляции – это вывод формулы магнитного поля прямолинейного проводника с током. С учетом симметрии в этой задаче контуром лучше выбрать окружность какого-то радиуса , лежащую в перпендикулярной проводнику плоскости. Центр окружности задан в какой-то точке проводника. Из-за симметрии вектор направляется по касательной , а его модуль имеет одинаковое значение по всей окружности. Использование теоремы о циркуляции приводит к выражению:
,
отсюда можно вывести формулу для модуля магнитной индукции поля прямолинейного проводника с током, приведенную раньше.
Из данного примера видно, что теорема о циркуляции вектора магнитной индукции можно использовать для вычисления магнитных полей, которые создаются симметричным распределением токов, когда можно наугад определить общую структуру поля.
Существует много примеров определения магнитных полей при помощи теоремы о циркуляции.
Рассмотрим одну из них – это задачу расчета поля тороидальной катушки (рисунок ).
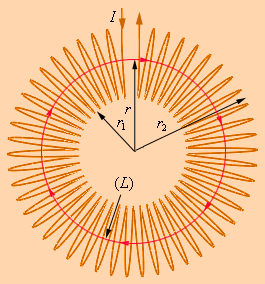
Рисунок Использование теоремы о циркуляции к тороидальной катушке.
Предположим, что катушка намотана виток к витку на ненамагниченный тороидальный сердечник. В ней линии магнитной индукции сходятся внутри катушки и выступают концентрическими окружностями. Они имеет такое направление, что, смотря вдоль них, наблюдатель увидел бы ток в витках, циркулирующих по часовой стрелке.
Одна линия индукции какого-то радиуса представлена на рисунке Используем теорему о циркуляции для контура в виде окружности, которая совпадает с линией индукции магнитного поля, изображенной на рисунке Опираясь на соображения о симметрии, делаем вывод, что модуль вектора имеет одинаковое значение по всей линии. Исходя из теоремы о циркуляции, запишем:
,
где – это полное количество витков, а – это ток, протекающий по виткам катушки. Значит, .
Так, модуль вектора магнитной индукции в тороидальной катушке находится в зависимости от радиуса . При условии, что сердечник катушки тонкий, то есть , тогда магнитное поле внутри катушки почти однородное.
Величина – это количество витков на единицу длины катушки. Следовательно, .
Сюда не относится радиус тора, потому оно действует и в предельном случае .
Однако в пределе каждая часть тороидальной катушки при необходимости рассматривается в качестве длинной прямолинейной катушки, которая называется соленоид. Вдали торцов такой катушки модуль магнитной индукции определяется, как соотношение в случае с тороидальной катушкой.
На рисунке представлено магнитное поле катушки конечной длины. Обращаем внимание, что в центре катушки магнитное поле почти однородное и намного сильнее, чем снаружи. Это объясняется густотой линий магнитной индукции. В предельном случае бесконечно длинного соленоида однородное магнитное поле полностью находится внутри него.
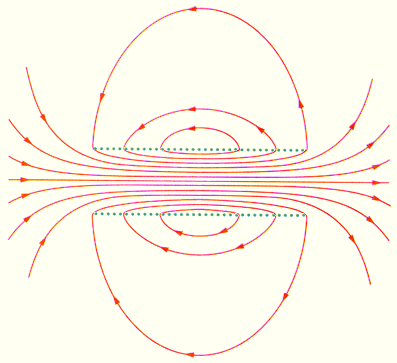
Рисунок Магнитное поле катушки конечной длины. В центральной части соленоида магнитное поле почти однородное и существенно больше по модулю поля вне катушки.
В случае с бесконечно длинным соленоидом соотношение для модуля магнитной индукции получаем прямо из теоремы о циркуляции, применяя ее к прямоугольному контуру, изображенному на рисунке
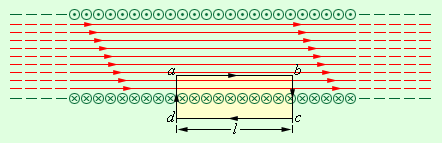
Рисунок Теорема о циркуляции при расчете магнитного поля бесконечно длинного соленоида.
Проекция вектора магнитной индукции на направление обхода контура только на стороне отлична от . Значит, циркуляция вектора по контуру равняется , где – это длина стороны . Количество витков соленоида, пронзающих контур , равняется , где – это количество витков на единицу длины соленоида, а полный ток, пронзающий контур, равняется . Из теоремы о циркуляции, .
Отсюда .
Данное вычисление совпадает с формулой для магнитного поля тонкой тороидальной катушки.
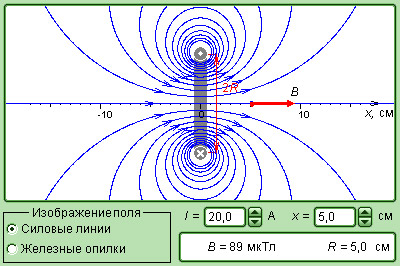
Рисунок Модель магнитного поля кругового витка с током.
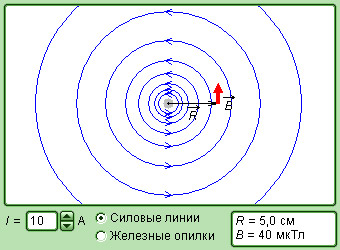
Рисунок Модель магнитного поля прямого тока.

Рисунок Модель магнитного поля соленоида.




