- 24 июля 2025
- 6 минут
- 3 741
Распределение Максвелла-Больцмана
Статью подготовили специалисты образовательного сервиса Zaochnik.
Распределение (или закон) Максвелла--Больцмана описывает распределение молекул газа по координатам и скоростям при системном воздействии внешнего потенциального поля.
Это распределение выводится из распределения Гиббса :
где – вероятность одного из состояний системы с энергией (полная энергия, состоящая из кинетической и потенциальной, которая присуща частицам). Рассмотрим чаще всего используемые формы распределения Максвелла-Больцмана.
Формы распределения Максвелла-Больцмана
Формула распределения для концентрации частиц
.
Здесь – количество частиц, присутствующих в выделенном объеме газа . Около точки, имеющей координаты , скорости молекул будут находиться в интервале от до . В указанной формуле есть наиболее вероятная скорость молекул; – является массой молекулы газа; – это потенциальная энергия частицы в точке с соответствующими координатами и, наконец, есть концентрация частиц газа в точке с потенциальной нулевой энергией.
Формула распределения для вероятности импульса и координаты
В данном выражении – переменная, показывающая вероятность нахождения частицы в фазовом объеме возле фазовой точки ; – потенциальная энергия молекулы внешнего поля. В данной формуле распределение Максвелла-Больцмана рассматривается в виде произведения двух вероятностей событий, не зависящих друг от друга: вероятность , что молекула имеет импульс и вероятность нахождения молекулы в точке . В таком случае выражение разложится на распределение Максвелла:
,
и распределение Больцмана:
.
Таким образом, распределения Максвелла и Больцмана служат составляющими элементами распределения Гиббса. Энергия молекул, движущихся в поле тяжести вверх, получает уменьшение, но в распределении Максвелла-Больцмана по скоростям средняя энергия при этом неизменна. Сохранность средней энергии частиц, когда происходит уменьшение энергии отдельно взятой молекулы, возможно благодаря выбыванию молекул с меньшей энергией из потока при увеличении высоты. Средняя энергия молекул, движущихся вниз, постоянна из-за присоединения к потоку молекул, выбывших из потока, направленного вверх.
Сходство между распределениями Максвелла и Больцмана
Распределения Максвелла и Больцмана обладают общей чертой: и в том и в другом случае законы включают в себя экспоненту, чей показатель в числителе содержит энергию молекулы (кинетическую у Максвелла, потенциальную у Больцмана), а в знаменателе имеют величину , определяющую среднюю энергию теплового движения молекул. Собственно, именно эта схожая черта и дает возможность объединять два распределения в один закон Максвелла-Больцмана.
Рассмотрим практические задачи на распределение Максвелла-Больцмана.
Пусть задан некий газ, имеющий неизменную массу, переводимый из одного равновесного состояния в другое. Необходимо определить, происходит ли изменение в распределении молекул по скоростям: положение максимума кривой в распределении Максвелла; площадь под этой кривой?
Решение
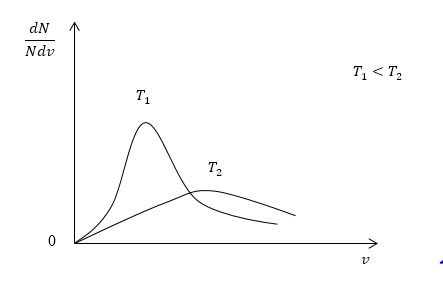
Рисунок
Составим запись распределения Максвелла по модулю скорости:
.
При переводе газа из одного равновесного состояния в другое имеет место изменение температуры газа. Таким образом, положение максимума кривой Максвелла изменится.
При этом в случае, когда температура увеличивается, максимум получит сдвиг в сторону больших скоростей, а величина пика (высота по вертикальной оси) уменьшится (рисунок ).
Площадь фигуры, ограниченной кривой и осью скоростей на рисунке , равна единице и останется постоянной при изменении температуры.
Необходимо определить количество молекул кислорода, чьи скорости находятся в пределах от до при температуре . Масса водорода .
Решение
Заданный условием скоростной интервал невелик, т.е. допустимо применять теорему о среднем, и тогда:
В данном выражении , , , .
Подставим полученное в :
.
Теперь в выражении применим конкретные числовые значения и осуществим расчет:
Ответ: искомое количество молекул кислорода в заданных условиях равно порядка .




