Уравнение состояния идеального газа. Изопроцессы

Содержание:

Преподаватель физики

Определение 1

Соотношение $p = n k T$ – это формула, связывающая значение давления газа с его температурой и концентрацией молекул на единицу объема.

Они взаимодействуют со стенками сосуда посредствам упругих соударений. Данное выражение можно записать иначе, учитывая параметрические состояния объема $V$ , давления $p$ , температуры $T$ и количества вещества $ν$ . Применим неравенства:

$n = \frac{N}{V} = \frac{ν N_{А}}{V} = \frac{m}{M} \frac{N_{A}}{V}$ .

Значением $N$ является количество молекул данного сосуда, $N_{А}$ – постоянной Авогадро, $m$ – массой газа в емкости, $М$ – молярной массой газа. Исходя из этого, формула примет вид:

$p V = ν N_{А} k T = \frac{m}{M} N_{А} k T$ .

Определение 2

Произведение постоянной Авогадро $N_{А}$ на постоянную Больцмана $k$ называют универсальной газовой постоянной и обозначают $R$ .

По системе $С И$ имеет значение $R = 8, 31 Д ж / м о л ь \cdot К$ .

Определение 3

Соотношение $p V = ν R T = \frac{m}{M} R T$ получило название уравнения состояния идеального газа.

Один моль газа обозначается $p V = R T$ .

Определение 4

При температуре $T_{н} = 273, 15 К (0 ° C)$ и давлении $ρ_{н} = 1 а т м = 1, 013 \cdot 10^{5} П а$ говорят о нормальных условиях состояния газа.

Определение 5

Из уравнения видно, что один моль газа при нормальных условиях занимает один и тот же объем, равный $v_{0} = 0, 0224 м^{3} / м о л ь = 22, 4 д м^{3} / м о л ь$ . Выражение получило название закона Авогадро.

Если имеется смесь невзаимодействующих газов, то формулу запишем как:

$p V = (ν_{1} + ν_{2} + ν_{3} + . . .) R T$ ,

где $ν_{1}, v_{2}, v_{3}$ обозначает количество вещества каждого из них.

Определение 6

Еще в ХХ веке Б. Клапейрон получил уравнение, показывающее связь между давлением и температурой:

$p V = ν R T = \frac{m}{M} R T$ .

Впоследствии оно было записано Д.И. Менделеевым. Позже его назвали уравнением Клапейрона-Менделеева.

Задолго до получения уравнения состояния идеального газа на основе молекулярно-кинетической теории поведения газов изучались в различных условиях экспериментально. То есть уравнение $p V = ν R T = \frac{m}{M} R T$ служит обобщением всех опытных фактов.

Газ принимает участие в процессах с постоянно изменяющимися параметрами состояния: ( $p, V$ и $T$ ).

Определение 7

При протекании процессов медленно, система находится в состоянии, близком к равновесному. Процесс получил название квазистатического.

Соотнеся с происхождением процессов в нашем времени, то его протекания нельзя считать медленными.

Определение 8

Обычное время для разрежения и сжатия газа сотни раз в секунду. Это рассматривается как квазистатический процесс. Они изображаются с помощью диаграммы состояний параметров, где каждая из точек показывает равновесное состояние.

Определение 9

При неизменном одном параметре из ( $p, V$ или $T$ ) процесс принято называть изопроцессом.

Изотермический процесс $(T = c o n s t)$

Определение 10

При протекании квазипроцесса с постоянным параметром $Т$ говорят об изотермическом процессе.

Из уравнения $p V = ν R T = \frac{m}{M} R T$ имеем, что неизменные температура $Т$ с количеством вещества $ν$ – это постоянное состояние для произведения значения давления газа $p$ на его объем $V$ :

$p V = c o n s t$ .

Изотермический процесс (T=const)

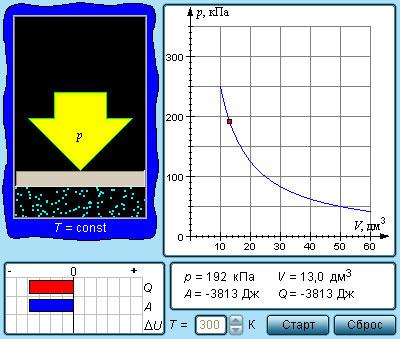
Рисунок $3.3.1 .$ Модель изотермического процесса.

Определение 11

Изображение изотермических процессов на плоскости $(p, V)$ предусматривает различные значения температур $Т$ гипербол $p ~ \frac{1}{V}$ . Они получили название изотермов.

Коэффициент пропорциональности данного отношения увеличивается с ростом $Т$ . Рисунок $3.3.2$ показывает, что при меньшей $Т$ подразумевает уменьшение $V$ . В $1662$ году было получено уравнение изотермического процесса Р. Бойлем, а позднее Э. Мариоттом в $1676$ году. Отсюда и сложное его название – закон Бойля-Мариотта.

Изотермический процесс (T=const)

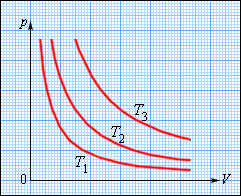
Рисунок $3.3.2 .$ Семейство изотерм на плоскости $(p, V)$ . $T_{3} > T_{2} > T_{1}$ .

Изохорный процесс $(V = c o n s t)$

Определение 12

Изохорный процесс – это квазипроцесс нагревания или охлаждения газа с постоянным параметром $V$ и неизменным количеством вещества $ν$ емкости.

Уравнение состояния идеального газа говорит о том, что изменение p газа происходит прямо пропорционально абсолютной температуры, тогда $p ~ T$ или $\frac{p}{T} = c o n s t$ .

Изохорный процесс (V=const)

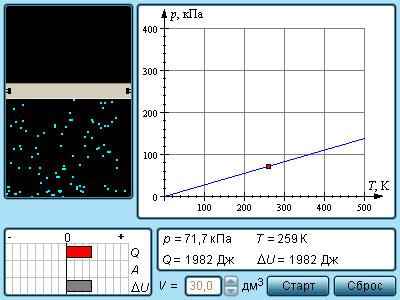
Рисунок $3.3.3 .$ Модель изохорного процесса.

Определение 13

Изохорные процессы плоскости $(p, T)$ с количеством вещества $ν$ и различными значениями параметра $V$ изображаются прямыми линиями – изохорами.

Рисунок $3.3.4$ говорит о наличии меньшего наклона оси $Т$ при увеличении параметра $V$ .

Изохорный процесс (V=const)

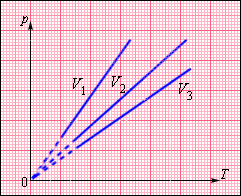
Рисунок $3.3.4 .$ Семейство изохор на плоскости $(p, T)$ . $V_{3} > V_{2} > V_{1}$ .

Определение 14

Экспериментальную зависимость параметра $p$ от $Т$ довелось исследовать физику Ж. Шарлю в $1787$ году. Позже уравнения изохорного процесса получило название закона Шарля.

Его запись принимает вид

$p = \frac{p_{0}}{T_{0}} T = p_{0} α T$ с $p_{0}$ ,

являющимся значением давления газа при $T = T_{0} = 273, 15 К$ (т.е. при температуре $0 ° C$ ). Температурный коэффициент давления обозначается $α = (\frac{1}{273, 15}) К^{- 1}$ .

Изобарный процесс $(p = c o n s t)$

Определение 15

Изобарный процесс – это квазистатический процесс, протекающий с постоянным параметром $p$ .

Уравнение такого состояния с неизменным количеством вещества $ν$ запишется как

$\frac{V}{T} = c o n s t$ или $V = V_{0} α T$ , где $V_{0}$ - объем газа при температуре $0 ° C$ . Температурный коэффициент объемного расширения газов равняется $α = (\frac{1}{273, 15}) К^{- 1}$ .

Изобарный процесс (p=const)

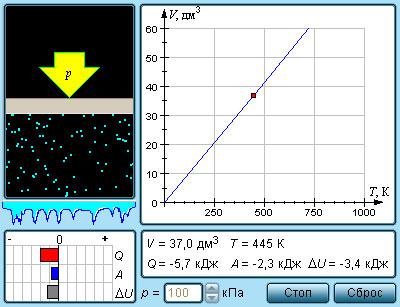
Рисунок $3.3.5 .$ Модель изобарного процесса.

Изобарные процессы плоскости $(V, T)$ имеют разные значения $p$ и изображены прямыми линиями (изобарами), изображенными на рисунке $3.3.6 .$

Изобарный процесс (p=const)

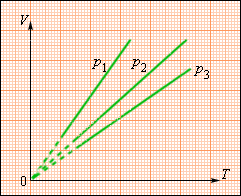
Рисунок $3.3.6 .$ Семейство изобар на плоскости $(V, T)$ . $p_{3} > p_{2} > p_{1}$ .

Определение 16

Данное уравнение с зависимостью параметра $V$ от $T$ с неизменным давлением довелось исследовать Ж. Гей-Люссаку в $1862$ году. Оно получило название закона Гей-Люссака.

Законы Бойла-Мариотта, Шарля и Гей-Люссака объясняются с помощью молекулярно-кинетической теории газов, так как являются следствиями уравнения состояния идеального газа.

Курсовая работа по физике

от 5 дней/ от 2160 р.

Реферат по физике

от 1 дня/ от 840 р.

Решение задач по физике

от 1 дня/ от 150 р.