Статью подготовили специалисты образовательного сервиса Zaochnik
Третий закон Ньютона
- 24 октября 2023
- 4 минуты
- 1 813
В этом разделе мы рассмотрим третий закон Ньютона, приведем подробные объяснения, познакомимся со значимыми понятиями, выведем формулу. Сухую теорию мы «разбавим» примерами и рисункам-схемами, которые облегчат усвоение темы.
В одном из прошлых разделов мы провели опыты по измерению ускорений двух тел после их взаимодействия и получили следующий результат: массы взаимодействующих друг с другом тел находятся в обратной зависимости с численными значениями ускорений. Так было введено понятие массы тела.
m1m2=-a2a1m1m2=−a2a1 или m1a1=-m2a2m1a1=−m2a2
Формулировка третьего закона Ньютона
Если придать этому соотношению векторную форму, получится:
m1→a1=-m2→a2m1→a1=−m2→a2
Знак минус в формуле появился неслучайно. Он свидетельствует о том, что ускорения двух тел, вступивших во взаимодействие, всегда направлены в противоположные стороны.
В качестве факторов, определяющих появление ускорения, согласно второму закону Ньютона, являются силы →F1=m1→a1−→F1=m1→a1 и →F2=m2→a2−→F2=m2→a2, которые возникают при взаимодействии тел.
Следовательно:
→F1=-→F2−→F1=−−→F2
Так мы получили фомулу третьего закона Ньютона.
Силы, с которыми тела вступают во взаимодействие друг с другом, равны по модулю и противоположны по направлению.
Природа сил, возникающих во время взаимодействия тел, одинакова. Эти силы приложены к разным телам, потому не могут уравновешивать друг друга. По правилам векторного сложения мы можем складывать только те силы, которые прилагаются к одному телу.
Третий закон Ньютона в примерах
Грузчик оказывает воздействие на некий груз с такой же по модулю силой, с какой этот груз воздействует на грузчика. Силы направлены в противоположные стороны. Физическая их природа одна и та же: упругие силы каната. Ускорение, которое сообщается каждому из тел из примера, обратно пропорционально массе тел.
Мы проиллюстрировали этот пример применения третьего закона Ньютона рисунком.
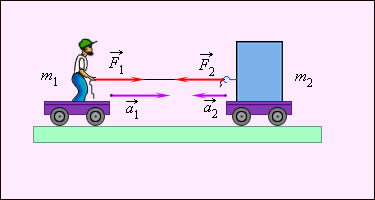
Рисунок 1.9.1.1.9.1. Третий закон Ньютона
→F1=-→F2·→a1=-m2m1→a2−→F1=−−→F2⋅→a1=−m2m1→a2
Силы, воздействующие на тело, могут быть внешними и внутренними. Введем необходимые для знакомства с темой третьего закона Ньютона определения.
Внутренние силы – это силы, которые действуют на различные части одного и того же тела.
Если мы рассматриваем тело, находящееся в движении, как единое целое, то ускорение этого тела будет определяться лишь внешней силой. Внутренние силы второй закон Ньютона не рассматривает, так как сумма их векторов равна нулю.
Предположим, что у нас есть два тела с массой m1m1 и m2m2. Эти тела жестко связаны между собой нитью, которая не имеет веса и не растягивается. Оба тела двигаются с одинаковым ускорением →a→a под воздействием некоторой внешней силы →F→F. Эти два тела движутся как единое целое.
Внутренние силы, которые действуют между телами, подчиняются третьему закону Ньютона: →F2=-→F1−→F2=−−→F1.
Движение каждого из тел в сцепке зависит от сил взаимодействия между этими телами. Если применить второй закон Ньютона к каждому из этих тел по отдельности, то мы получим: m1→a1=→F1, m2→a1=→F2+→Fm1→a1=−→F1, m2→a1=−→F2+→F.
Мы можем сложить правую и левую части этих уравнений, приняв во внимание, что →a1=→a2=→a→a1=→a2=→a и →F2=-→F1−→F2=−−→F1.
Получим: (m1+m2)→a=→F1(m1+m2)→a=−→F1.
Как видите, внутренние силы исключились из уравнения движения системы двух связанных тел.
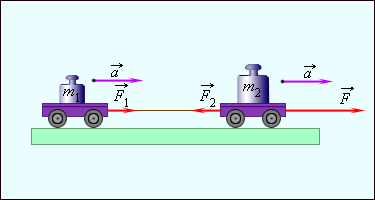
Рисунок 1.9.2.1.9.2. Исключение внутренних сил.
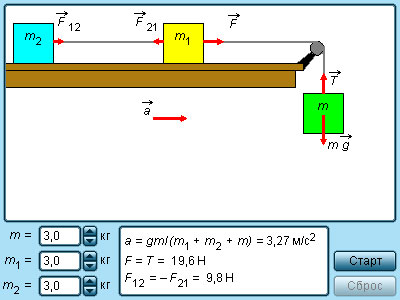
Рисунок 1.9.3.1.9.3. Модель движения связанных брусков.
Сохранить статью удобным способом
