- 24 июля 2025
- 9 минут
- 3 985
Преобразования Лоренца
Статью подготовили специалисты образовательного сервиса Zaochnik.
Ранее мы уже изучили формулы, называемые классическими преобразованиями Галилея, однако они несовместимы с постулатами специальной теории относительности (СТО). Поэтому в данном случае нам нужно использовать другие положения. Благодаря новым преобразованиям мы сможем установить, какая связь существует между некоторым моментом события , наблюдаемого в системе отсчета в точке с координатами и показателями того же события, которое наблюдается в системе отсчета .
Преобразования Лоренца представляют собой кинематические формулы, с помощью которых происходит преобразование координат и времени в специальной теории относительности.
Они были впервые сформулированы еще в году в качестве преобразований, относительно которых были инвариантны уравнения электродинамики.
Обозначим основные системы и , скорость их движения – , а ось, вдоль которой они движутся – . В таком случае преобразования Лоренца примут следующий вид:
.
Используя эти формулы, мы можем вывести из них множество следствий. Так, именно из системы преобразований Лоренца следует лоренцево сокращение длины и релятивистский эффект замедления времени.
Возьмем случай, когда в системе происходит некий процесс, длительность которого составляет (по собственному времени). Здесь и – это время на часах в начале данного процесса и в его конце. Чтобы вычислить его общую продолжительность в точке , необходимо взять для расчета следующую формулу:
.
Формула релятивистского сокращения длины выводится из преобразований Лоренца точно таким же образом.
Принцип относительности одновременности
Еще одно важное следствие, которое необходимо знать, – это положение о том, что любая одновременность относительна.
Например, если в системе отсчета взять две разные точки, в которых некий процесс будет протекать одновременно (с позиции стороннего наблюдателя), то в системе наблюдатель будет иметь следующее:
Из этого вытекает пространственная разобщенность данных событий в системе , следовательно, они не могут считаться одновременными. Нельзя сразу сказать, какое событие будет происходить первым, а какое вторым, поскольку это определяется особенностями системы отсчета – знак разности будет определен знаком выражения .
Если между событиями имеется причинно-следственная связь, то данный вывод специальной теории относительности для них использовать нельзя. Однако мы можем показать, что при этом не нарушается принцип причинности, и события следуют в нужном порядке в любой инерциальной системе отсчета.
Разберем пример, показывающий, что одновременность разобщенных в пространстве событий является относительной.
Возьмем систему отсчета и расположим в ней длинный жесткий стержень. Его положение будет неподвижным и ориентированным вдоль оси абсцисс. Установим на оба его конца часы, синхронизированные между собой, а в центр поместим импульсную лампу. Также у нас будет система , совершающая движение вдоль оси x в системе .
В определенный момент времени лампа включится и пошлет световые сигналы в направлении обоих концов жесткого стержня. Поскольку она находится точно в центре, эти сигналы должны дойти до концов в одно и то же время , которое должно быть зафиксировано расположенными на них часами. Однако концы стержня движутся относительно системы так, что один конец стремится навстречу световому сигналу, а другой конец свету приходится догонять. Скорость света, распространяющегося в оба направления, одинакова, но сторонний наблюдатель скажет, что до левого конца свет дошел быстрее, чем до правого.
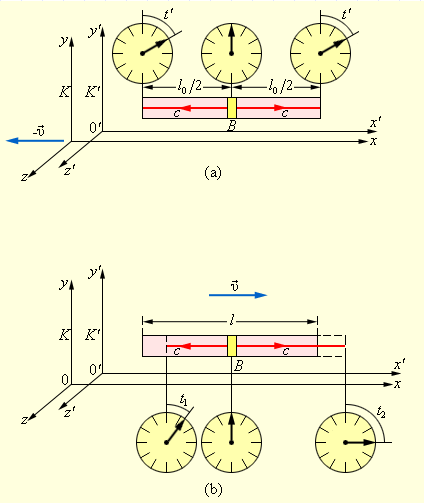
Рисунок Иллюстрация принципа относительности одновременности: достижение световым импульсом концов стержня в системе в одно и то же время и в системе в разное.
Инвариантные величины в СТО
Данные преобразования нужны нам для выражения относительного характера временных промежутков и промежутков расстояний. Вместе с тем в специальной теории относительности помимо утверждения относительного характера времени и пространства очень важно установить инвариантные физические величины, не изменяющиеся при смене системы отсчета. Подобной величиной является скорость света в вакууме, чей характер в рамках СТО становится абсолютным. Также важна такая величина, как интервал между событиями, поскольку именно она выражает абсолютность пространственно-временной связи.
Для вычисления пространственно-временного интервала необходимо использовать следующую формулу:
.
В ней с помощью параметра выражено расстояние между точками одной системы, где совершаются события, а – это временной промежуток между теми же самыми событиями. Если местом одного из событий является начало координат, т.е. и , а второе происходит в точке с координатами в некоторое время , то формула вычисления пространственно-временного интервала между ними записывается так:
.
Преобразования Лоренца дают нам возможность доказать неизменность пространственно-временного интервала между событиями при смене инерциальной системы.
Если величина интервала не зависит от того, какая система отсчета используется, т.е. является объективной при любых относительных расстояниях и временных промежутках, то такой интервал называется инвариантным.
Допустим, что у нас есть событие (вспышка света), которое произошло в точке начала координат в некоторой системе во время, равное , а потом свет переместился в другую точку с координатами во время . Тогда мы можем записать следующее:
.
У нас получилось, что интервал этой пары событий будет равен нулю. Если мы поменяем систему координат и возьмем другое время для второго события, то результаты окажутся точно такими же, поскольку:
Иначе говоря, любые два события, которые связывает между собой световой сигнал, будут иметь нулевой пространственно-временной интервал.
Также формулы Лоренца для времени и координат можно использовать для выведения релятивистского закона сложения скоростей.
Например, у нас есть частица, которая находится в системе отсчета и движется в ней вдоль оси абсцисс со скоростью . Параметры скорости и равны . В системе , соответственно, скорость будет равна .
Применим к одной из формул преобразования Лоренца операцию дифференцирования и получим следующее:
.
Данные отношения являются выражением релятивистского закона сложения скоростей. Он применим в случае движения частицы параллельно относительной скорости в системах отсчета и .
Если , то релятивистские отношения могут быть преобразованы в формулы классической механики:
.
Если мы имеем дело со световым импульсом, распространяющимся в системе вдоль оси со скоростью , то в этом случае применима следующая формула:
.
Иначе говоря, скорость распространения светового импульса в системе вдоль оси также будет равна , что соответствует постулату об инвариантности скорости света.




