Классическая электронная теория дисперсии

Содержание:

Преподаватель физики

Определение 1

Дисперсией называется зависимость скорости распространения волны от ее частоты.

Явление дисперсии света

Определение 2

Дисперсия света – это результат взаимодействия электромагнитных волн (световых волн) с заряженными частицами, составляющими вещество совместно с нейтральными частицами.

При таком явлении происходит спектральное разложение немонохроматического света на синусоидальные составляющие. Осуществляется это потому, что для разных частот соответствуют различные показатели преломления. В вакууме каждая электромагнитная волна распространяется с одинаковой скоростью вне зависимости от своей частоты. Явление дисперсии возможно только лишь в веществе. Следовательно, ее объяснение связано со структурой вещества, которое дает классическая электронная теория дисперсии света.

Существенная разница между $ε^{2}$ ( $ε$ – диэлектрической проницаемостью вещества) и $n$ (показателем преломления среды) наблюдается у веществ с полярными молекулами, если $ε$ измеряется на частотах существенно отличающихся от частоты волн света. Но замеры показателей преломления веществ в оптическом диапазоне показывают, что показатель $n$ одинаковый у веществ с полярными и неполярными молекулами. Это означает, что ориентационная поляризуемость имеется в веществах с полярными молекулами в статическом поле либо переменных полях малой частоты. Иза-за того что в высокочастотных полях молекулярный диполь не успевает поворачиваться, степень ориентации диполей снижается, поэтому снижается и диэлектрическая проницаемость. Рассмотрим основные положения электронной теории дисперсии.

Закон дисперсии

Чтобы понять зависимость показателя преломления вещества от частоты (т. е. явление дисперсии) проведем анализ механизма поляризации атома (молекулы) в электромагнитном поле волны света.

Электрическая составляющая электромагнитной волны оказывает действие на электрон. Действием магнитной составляющей, как правило, пренебрегают, поскольку скорость электрона маленькая по сравнению со скоростью света. Электрическая сила, с которой волна воздействует на оптический электрон и заставляет их колебаться, имеет важное практическое значение в электронной теории дисперсии.

Выводя закон дисперсии, мы учли только лишь действие внешнего поля световой волны на электронное облако молекулы и не принимали во внимание межмолекулярное взаимодействие. Следовательно, закон выполняется только лишь применительно к газам. Однако для качественного пояснения процесса дисперсии он применяется для жидких и твердых тел. Помимо этого, закон дисперсии имеет смысл только при условии, что частота волны значительно отличается от собственной частоты колебаний электрона.

График закона дисперсии изображен на рисунке $1$ . Более точная теория дисперсии, учитывающая затухание и приводящая к верной зависимости показателя преломления на всем диапазоне частот, представлена на графике, изображенном сплошной линией на рисунке $1$ .

Закон дисперсии

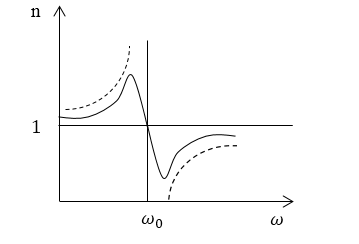
Рисунок $1$

Пример 1

Необходимо определить концентрацию свободных электронов в ионосфере, если показатель преломления равняется $n$ для радиоволн с частотой $ν$ .

Решение

Для решения задачи возьмем выражение:

$n^{2} = 1 + \frac{n_{0} {q_{e}}^{2}}{m ε_{0} (ω_{0}^{2} - ω^{2})} (1.1)$ ,

где $n_{0}$ – это концентрация молекул.

Будем учитывать, что для свободных электронов собственная частота равняется $0$ $(ω_{0}^{2} = 0)$ . Частота $ν$ и циклическая частота $(ω)$ связаны между собой таким образом:

$ω = 2 π ν (1.2)$ .

Значит, формулу $(1.1)$ приведем к виду:

$n^{2} = 1 - \frac{n_{0} {q_{e}}^{2}}{m ε_{0} {(2 πν)}^{2}} (1.3)$ .

Из выражения $(1.3)$ получается:

$n_{0} = \frac{(1 - n^{2}) m ε_{0} {(2 π ν)}^{2}}{{q_{e}}^{2}}$ .

Ответ: $n_{0} = \frac{(1 - n^{2}) m ε_{0} {(2 π ν)}^{2}}{{q_{e}}^{2}}$ .

Пример 2

В каждом теле наблюдается не одна, а несколько полос поглощения. Чтобы это учесть, в классической теории считают, что вещество состоит из частиц различного типа (электронов, ионов). Причем частицы ведут себя в качестве затухающих гармонических осцилляторов, имеющих различные собственные частоты. В разреженных газах взаимодействием данных частиц пренебрегают. Как записывается выражение для коэффициента преломления такого вещества в соответствии с классической теорией дисперсии? Какой вывод можно сделать о поведении полученного выражения?

Решение

Для решения задачи возьмем выражение для одного типа частиц вида:

$n^{2} = 1 + \frac{n_{0} {q_{e}}^{2}}{m ε_{0} (ω_{0}^{2} - ω^{2})} (1.1)$ .

Тогда искомую формулу можно представить следующим образом:

$n^{2} = 1 + \frac{n_{0}}{ε_{0}} \sum_{k} \frac{{q_{e}}^{2}}{m (ω_{0 k}^{2} - ω^{2})} (1.2)$ ,

где $ω_{k 0}$ – это собственные частоты частиц, из которых состоит газ. Около каждой собственной частоты функция, находящаяся в $(1.2)$ , разрывается. Если $ω$ стремится к $ω_{k 0}$ слева, тогда функция $n (ω)$ стремится к $+ \infty$ . Если $ω$ стремится к $ω_{k 0}$ справа, тогда $n (ω) \to - \infty$ . Это поведение функции объяснимо тем, что если пренебречь трением, амплитуда вынужденных колебаний при резонансе стремится к бесконечности.

Курсовая работа по физике

от 5 дней/ от 2160 р.

Реферат по физике

от 1 дня/ от 840 р.

Решение задач по физике

от 1 дня/ от 150 р.