Деление целых чисел с остатком: правила, примеры

Содержание:

02 марта 2023
15 минут
1599

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Статья разбирает понятие деления целых чисел с остатком. Докажем теорему о делимости целых чисел с остатком и просмотрим связи между делимыми и делителями, неполными частными и остатками. Рассмотрим правила, когда производится деление целых чисел с остатками, рассмотрев подробно на примерах. В конце решения выполним проверку.

Общее представление о делении целых чисел с остатками

Деление целых чисел с остатком рассматривается как обобщенное деление с остатком натуральных чисел. Это выполняется потому, что натуральные числа – это составная часть целых.

Деление с остатком произвольного числа говорит о том, что целое число $a$ делится на число $b$ , отличное от нуля. Если $b = 0$ , тогда не производят деление с остатком.

Также как и деление натуральных чисел с остатком, производится деление целых чисел $a$ и $b$ , при $b$ отличном от нуля, на $c$ и $d$ . В этом случае $a$ и $b$ называют делимым и делителем, а $d$ – остатком деления, $с$ – целое число или неполное частное.

Если считать, что остаток – это целое неотрицательное число, тогда его величина не больше модуля числа $b$ . Запишем таким образом: $0 \leq d \leq |b|$ . Данная цепочка неравенств используется при сравнении $3$ и более количества чисел.

Если $с$ – неполное частное, тогда $d$ – остаток от деления целого числа $a$ на $b$ , кратко можно зафиксировать: $a : b = c$ (ост. $d$ ).

Остаток при делении чисел $a$ на $b$ возможен нулевой, тогда говорят, что $a$ делится на $b$ нацело, то есть без остатка. Деление без остатка считается частным случаем деления.

Если делим ноль на некоторое число, получаем в результате ноль. Остаток деления также будет равен нулю. Это можно проследить из теории о делении нуля на целое число.

Теперь рассмотрим смысл деления целых чисел с остатком.

Известно, что целые положительные числа – натуральные, тогда при делении с остатком получится такой же смысл, как и при делении натуральных чисел с остатком.

При делении целого отрицательного числа а на целое положительное $b$ имеется смысл. Рассмотрим на примере. Представив ситуацию, когда имеем долг предметов в количестве $|a|$ , которое необходимо погасить $b$ человек. Для этого необходимо каждому внести одинаковый вклад. Чтобы определить величину долга для каждого, необходимо обратить внимание на величину частного $с$ . Остаток $d$ говорит о том, что известно количество предметов после расплаты с долгами.

Рассмотрим на примере с яблоками. Если $2$ человека должны $7$ яблок. В случае, если посчитать, что каждый должен вернуть по $4$ яблока, после полного расчета у них останется 1 яблоко. Запишем в виде равенства это: $(- 7) : 2 = - 4 (о с т . 1)$ .

Деление любого числа а на целое не имеет смысла, но возможно как вариант.

Теорема о делимости целых чисел с остатком

Мы выявили, что $а$ – это делимое, тогда $b$ – это делитель, $с$ – неполное частное, а $d$ – остаток. Они между собой связаны. Эту связь покажем при помощи равенства $a = b \cdot c + d$ . Связь между ними характеризуется теоремой делимости с остатком.

Теорема

Любое целое число может быть представлено только через целое и отличное от нуля число $b$ таким образом: $a = b \cdot q + r$ , где $q$ и $r$ – это некоторые целые числа. Тут имеем $0 \leq r \leq |b|$ .

Докажем возможность существования $a = b \cdot q + r$ .

Доказательство

Если существуют два числа $a$ и $b$ , причем $a$ делится на $b$ без остатка, тогда из определения следует, что имеется число $q$ , что будет верно равенство $a = b \cdot q$ . Тогда равенство можно считать верным: $a = b \cdot q + r$ при $r = 0$ .

Если посчитать, что $b$ – целое положительное число, тогда, следует выбрать целое $q$ так, чтобы произведение $b \cdot q$ не было больше значения числа $а$ , а произведение $b \cdot (q + 1)$ было больше, чем $a$ .

Тогда необходимо взять $q$ такое, чтобы данное неравенством $b \cdot q < a < b \cdot (q + 1)$ было верным. Необходимо вычесть $b \cdot q$ из всех частей выражения. Тогда придем к неравенству такого вида: $0 < a - b \cdot q < b$ .

Имеем, что значение выражения $a - b \cdot q$ больше нуля и не больше значения числа b, отсюда следует, что $r = a - b \cdot q$ . Получим, что число а можем представить в виде $a = b \cdot q + r$ .

Теперь необходимо рассмотреть возможность представления $a = b \cdot q + r$ для отрицательных значений $b$ .

Модуль числа получается положительным, тогда получим $a = |b| \cdot q_{1} + r$ , где значение $q_{1}$ –некоторое целое число, $r$ – целое число, которое подходит условию $0 \leq r < |b|$ . Принимаем $q = - q_{1}$ , получим, что $a = b \cdot q + r$ для отрицательных $b$ .

Доказательство единственности

Допустим, что $a = b \cdot q + r$ , $q$ и $r$ являются целыми числами с верным условием $0 \leq r < |b|$ , имеется еще одна форма записи в виде $a = b \cdot q_{1} + r_{1}$ , где $q_{1}$ и $r_{1}$ являются некоторыми числами, где $q_{1} \neq q$ , $0 \leq r_{1} < |b|$ .

Когда из левой и правых частей вычитается неравенство, тогда получаем $0 = b \cdot (q - q_{1}) + r - r_{1}$ , которое равносильно $|r - r_{1}| = |b \cdot (q_{1} - q)|$ . Так как используется модуль, получим равенство $|r - r_{1}| = |b| \cdot |q_{1} - q|$ .

Заданное условие говорит о том, что $0 \leq r < |b|$ и $0 \leq r_{1} < |b|$ запишется в виде $|r - r_{1}| < |b|$ . Имеем, что $q$ и $q_{1}$ – целые, причем $q \neq q_{1}$ , тогда $|q_{1} - q| \geq 1$ . Отсюда имеем, что $|b| \cdot |q_{1} - q| \geq |b|$ . Полученные неравенства $|r - r_{1}| < |b|$ и $|b| \cdot |q_{1} - q| \geq |b|$ указывают на то, что такое равенство в виде $|r - r_{1}| = |b| \cdot |q_{1} - q|$ невозможно в данном случае.

Отсюда следует, что по-другому число $a$ быть представлено не может, кроме как такой записью $a = b \cdot q + r$ .

Связь между делимым, делителем, неполным частным и остатком

При помощи равенства $a = b \cdot c + d$ можно находить неизвестное делимое $a$ , когда известен делитель $b$ с неполным частным $c$ и остатком $d$ .

Пример 1

Определить делимое, если при деление получим $- 21$ , неполное частное $5$ и остаток $12$ .

Решение

Необходимо вычислить делимое $a$ при известном делителе $b = - 21$ , неполным частным $с = 5$ и остатком $d = 12$ . Нужно обратиться к равенству $a = b \cdot c + d$ , отсюда получим $a = (- 21) \cdot 5 + 12$ . При соблюдении порядка выполнения действий умножим $- 21$ на $5$ , после этого получаем $(- 21) \cdot 5 + 12 = - 105 + 12 = - 93$ .

Ответ: $- 93$ .

Связь между делителем и неполным частным и остатком можно выразить при помощи равенств: $b = (a - d) : c$ , $c = (a - d) : b$ и $d = a - b \cdot c$ . С их помощью мы можем вычислить делитель, неполное частное и остаток. Это сводится к постоянному нахождению остатка от деления целого целых чисел $a$ на $b$ с известным делимым, делителем и неполным частным. Применяется формула $d = a - b \cdot c$ . Рассмотрим решение подробно.

Пример 2

Найти остаток от деления целого числа $- 19$ на целое $3$ при известном неполном частном равном $- 7$ .

Решение

Чтобы вычислить остаток от деления, применим формулу вида $d = a - b \cdot c$ . По условию имеются все данные $a = - 19, b = 3, c = - 7$ . Отсюда получим $d = a - b \cdot c = - 19 - 3 \cdot (- 7) = - 19 - (- 21) = - 19 + 21 = 2$ (разность $- 19 - (- 21)$ . Данный пример вычислен по правилу вычитания целого отрицательного числа.

Ответ: $2$ .

Деление с остатком целых положительных чисел, примеры

Все целые положительные числа являются натуральными. Отсюда следует, что деление выполняется по всем правилам деления с остатком натуральных чисел. Скорость выполнения деления с остатком натуральных чисел важна, так как на нем основано не только деление положительных, но и правила деления целых произвольных.

Самый удобный метод деления – это столбик, так как проще и быстрее получить неполное или просто частное с остатком. Рассмотрим решение более подробно.

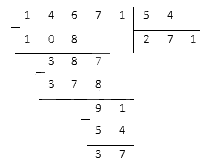
Деление с остатком целых положительных чисел, примеры — Пример 3

Правило деления с остатком целого положительного числа на целое отрицательное, примеры

Чтобы выполнить деление с остатком положительного числа на целое отрицательное, необходимо сформулировать правило.

Определение 1

Неполное частное от деления целого положительного $a$ на целое отрицательное $b$ получаем число, которое противоположно неполному частному от деления модулей чисел $a$ на $b$ . Тогда остаток равен остатку при делении $|a|$ на $|b|$ .

Отсюда имеем, что неполное частное от деления целого полодительного числа на целое отрицательное число считают целым неположительным числом.

Получим алгоритм:

найти модули делимого и делителя;
делить модуль делимого на модуль делителя, тогда получим неполное частное и
остаток;
запишем число противоположное полученному.

Рассмотрим на примере алгоритма деления целого положительного числа на целое отрицательное.

Пример 4

Выполнить деление с остатком $17$ на $- 5$ .

Решение

Применим алгоритм деления с остатком целого положительного числа на целое отрицательное. Необходимо разделить $17$ на $- 5$ по модулю. Отсюда получим, что неполное частное равно $3$ , а остаток равен $2$ .

Получим, что искомое число от деления $17$ на $- 5 = - 3$ с остатком равным $2$ .

Ответ: $17 : (- 5) = - 3$ (ост. $2$ ).

Пример 5

Необходимо разделить $45$ на $- 15$ .

Решение

Необходимо разделить числа по модулю. Число $45$ делим на $15$ , получим частное $3$ без остатка. Значит, число $45$ делится на $15$ без остатка. В ответе получаем $- 3$ , так как деление производилось по модулю.

$45 : (- 15) = (|45| : |- 15|) = - (45 : 15) = - 3$

Ответ: $45 : (- 15) = - 3$ .

Деление с остатком целого отрицательного числа на целое положительное, примеры

Формулировка правила деления с остатком выглядит следующим образом.

Определение 2

Для того, чтобы получить неполное частное с при делении целого отрицательного $a$ на положительное $b$ , нужно применить противоположное данному числу и вычесть из него $1$ , тогда остаток $d$ будет вычисляться по формуле: $d = a - b \cdot c$ .

Исходя из правила можно сделать вывод, что при делении получим целое неотрицательное число. Для точности решения применяют алгоритм деления $а$ на $b$ с остатком:

найти модули делимого и делителя;
делить по модулю;
записать противоположное данному число и вычесть $1$ ;
использовать формулу для остатка $d = a - b \cdot c$ .

Рассмотрим на примере решения, где применяется данный алгоритм.

Пример 6

Найти неполное частное и остаток от деления $- 17$ на $5$ .

Решение

Делим заданные числа по модулю. Получаем, что при делении частное равно $3$ , а остаток $2$ . Так как получили $3$ , противоположное $- 3$ . Необходимо отнять $1$ .

$- 3 - 1 = - 4$ .

Искомое значение полчаем равное $- 4$ .

Чтобы вычислить остаток, необходимо $a = - 17, b = 5, c = - 4$ , тогда $d = a - b \cdot c = - 17 - 5 \cdot (- 4) = - 17 - (- 20) = - 17 + 20 = 3$ .

Значит, неполным частным от деления является число $- 4$ с остатком равным $3$ .

Ответ: $(- 17) : 5 = - 4$ (ост. $3$ ).

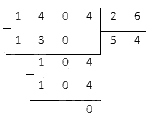
Деление с остатком целого отрицательного числа на целое положительное, примеры — Пример 7

Правило деления с остатком целых отрицательных чисел, примеры

Необходимо сформулировать правило деления с остатком целых отрицательных чисел.

Определение 3

Для получения неполного частного с от деления целого отрицательного числа $a$ на целое отрицательное $b$ , необходимо произвести вычисления по модулю, после чего прибавить $1$ , тогда сможем произвести вычисления по формуле $d = a - b \cdot c$ .

Отсюда следует, что неполное частное от деления целых отрицательных чисел будет число положительное.

Сформулируем данное правило в виде алгоритма:

найти модули делимого и делителя;
разделить модуль делимого на модуль делителя с получением неполного частного с
остатком;
прибавление $1$ к неполному частному;
вычисление остатка, исходя из формулы $d = a - b \cdot c$ .

Данный алгоритм рассмотрим на примере.

Пример 8

Найти неполное частное и остаток при делении $- 17$ на $- 5$ .

Решение

Для правильности решения применим алгоритм для деления с остатком. Для начала раздели числа по модулю. Отсюда получим, что неполное частное $= 3$ , а остаток равен $2$ . По правилу необходимо сложить неполное частное и $1$ . Получим, что $3 + 1 = 4$ . Отсюда получим, что неполное частное от деления заданных чисел равно $4$ .

Для вычисления остатка мы применим формулу. По условию имеем, что $a = - 17, b = - 5, c = 4$ , тогда, используя формулу, получим $d = a - b \cdot c = - 17 - (- 5) \cdot 4 = - 17 - (- 20) = - 17 + 20 = 3$ . Искомый ответ, то есть остаток, равен $3$ , а неполное частное равно $4$ .

Ответ: $(- 17) : (- 5) = 4$ (ост. $3$ ).

Проверка результата деления целых чисел с остатком

После выполнение деления чисел с остатком необходимо выполнять проверку. Данная проверка подразумевает $2$ этапа. Вначале идет проверка остатка $d$ на неотрицательность, выполнение условия $0 \leq d < |b|$ . При их выполнении разрешено выполнять $2$ этап. Если $1$ этап не выполнился, значит вычисления произведены с ошибками. Второй этап состоит из того, что равенство $a = b \cdot c + d$ должно быть верным. Иначе в вычисления имеется ошибка.

Рассмотрим на примерах.

Пример 9

Произведено деление $- 521$ на $- 12$ . Частное равно $44$ , остаток $7$ . Выполнить проверку.

Решение

Так как остаток – это число положительное, то его величина является меньше, чем модуль делителя. Делитель равен $- 12$ , значит, его модуль равен $12$ . Можно переходить к следующему пункту проверки.

По условию имеем, что $a = - 521$ , $b = - 12$ , $c = 44$ , $d = 7$ . Отсюда вычислим $b \cdot c + d$ , где $b \cdot c + d = - 12 \cdot 44 + 7 = - 528 + 7 = - 521$ . Отсюда следует, что равенство верное. Проверка пройдена.

Пример 10

Выполнить проверку деления $(- 17) : 5 = - 3$ (ост. $- 2$ ). Верно ли равенство?

Решение

Смысл первого этапа заключается в том, что необходимо проверить деление целых чисел с остатком. Отсюда видно, что действие произведено неверно, так как дан остаток, равный $- 2$ . Остаток не является отрицательным числом.

Имеем, что второе условие выполненное, но недостаточное для данного случая.

Ответ: нет.

Пример 11

Число $- 19$ разделили на $- 3$ . Неполное частное равно $7$ , а остаток $1$ . Проверить, верно ли выполнено данное вычисление.

Решение

Дан остаток, равный $1$ . Он положительный. По величине меньше модуля делителя, значит, первый этап выполняется. Перейдем ко второму этапу.

Вычислим значение выражения $b \cdot c + d$ . По условию имеем, что $b = - 3, c = 7, d = 1$ , значит, подставив числовые значения, получим $b \cdot c + d = - 3 \cdot 7 + 1 = - 21 + 1 = - 20$ . Следует, что $a = b \cdot c + d$ равенство не выполняется, так как в условии дано $а = - 19$ .

Отсюда следует вывод, что деление произведено с ошибкой.

Ответ: нет.

Курсовая работа по математике

от 5 дней/ от 2160 р.

Реферат по математике

от 1 дня/ от 840 р.

Решение задач по математике

от 1 дня/ от 150 р.