Основное свойство дроби: формулировка, доказательство, примеры применения

3 апреля 2023
4 минуты
1 937

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

В данной статье разберем, в чем заключается основное свойство дроби, сформулируем его, приведем доказательство и наглядный пример. Затем рассмотрим, как применять основное свойство дроби при совершении действий сокращения дробей и приведения дробей к новому знаменателю.

Основное свойство дроби, формулировка, доказательство и примеры

Все обыкновенные дроби обладают важнейшим свойством, которое мы и называем основным свойством дроби, и звучит оно следующим образом:

Определение 1

Если числитель и знаменатель одной дроби умножить или разделить на одно и то же натуральное число, то в итоге получится дробь, равная заданной.

Представим основное свойство дроби в виде равенства. Для натуральных чисел $a, b$ и $m$ будут справедливыми равенства:

$\frac{a \cdot m}{b \cdot m} = \frac{a}{b}$ и $\frac{a : m}{b : m} = \frac{a}{b}$

Рассмотрим доказательство основного свойства дроби. Опираясь на свойства умножения натуральных чисел и свойства деления натуральных чисел, запишем равенства: $(a \cdot m) \cdot b = (b \cdot m) \cdot a$ и $(a : m) \cdot b = (b : m) \cdot a$ . Таким образом, дроби $\frac{a \cdot m}{b \cdot m}$ и $\frac{a}{b}$ , а также $\frac{a : m}{b : m}$ и $\frac{a}{b}$ являются равными по определению равенства дробей.

Разберем пример, который графически проиллюстрирует основное свойство дроби.

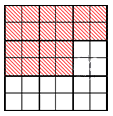
Основное свойство дроби, формулировка, доказательство и примеры — Пример 1

Чтобы закрепить теорию, разберем решение примера.

Пример 2

Задано, что числитель и знаменатель некоторой обыкновенной дроби умножили на $47$ , после чего эти числитель и знаменатель разделили на $3$ . Равна ли полученная в итоге этих действий дробь заданной?

Решение

Опираясь на основное свойство дроби, можно говорить о том, что умножение числителя и знаменателя заданной дроби на натуральное число $47$ даст в результате дробь, равную исходной. То же самое мы можем утверждать, производя дальнейшее деление на $3$ . В конечном счете мы получим дробь, равную заданной.

Ответ: да, полученная в итоге дробь будет равна исходной.

Применение основного свойства дроби

Основное свойство применяется, когда нужно привести дроби к новому знаменателю и при сокращении дробей.

Приведение дроби к новому знаменателю – это действие замены заданной дроби равной ей дробью, но с большими числителем и знаменателем. Чтобы привести дробь к новому знаменателю, нужно умножить числитель и знаменатель дроби на необходимое натуральное число. Действия с обыкновенными дробями были бы невозможны без способа приводить дроби к новому знаменателю.

Определение 2

Сокращение дроби – действие перехода к новой дроби, равной заданной, но с меньшими числителем и знаменателем. Чтобы сократить дробь, нужно разделить числитель и знаменатель дроби на одно и то же необходимое натуральное число, которое будет называться общим делителем.

Возможны случаи, когда подобного общего делителя нет, тогда говорят о том, что исходная дробь несократима или не подлежит сокращению. В частности, сокращение дроби при помощи наибольшего общего делителя приведет дробь к несократимому виду.