Статью подготовили специалисты образовательного сервиса Zaochnik
Перевод десятичной дроби в обыкновенную и наоборот: правило, примеры
- 25 июня 2023
- 18 минут
- 5 549
Бывает, что для удобства расчетов нужно перевести обыкновенную дробь в десятичную и наоборот. О том, как это делать, мы поговорим в данной статье. Разберем правила перевода обыкновенных дробей в десятичные и обратно, а также приведем примеры.
Перевод обыкновенных дробей в десятичные
Мы будем рассматривать перевод обыкновенных дробей в десятичные, придерживаясь определенной последовательности. Во первых, рассмотрим, как в десятичные переводятся обыкновенные дроби со знаменателем, кратным 10: 10, 100, 1000 и т.д.Дроби с такими знаменателями, по сути, являются, более громоздкой записью десятичных дробей.
Далее мы рассмотрим, как переводить в десятичные дроби обыкновенные дроби с любым, не только кратным 10, знаменателем. Отметим, что при обращении обыкновенных дробей в десятичные получаются не только конечные десятичные, но и бесконечные периодические десятичные дроби.
Приступим!
Перевод обыкновенных дробей со знаменателями 10, 100, 1000 и т.д. в десятичные дроби
Первым делом, скажем, что некоторые дроби нуждаются в определенной подготовке перед обращением в десятичный вид. В чем она заключается? Перед цифрой, стоящей в числителе, необходимо дописать столько нулей, чтобы количество цифр числителя стало равно числу нулей в знаменателе. Например, для дроби 3100 число 0 необходимо один раз дописать слева от 3 в числителе. Дробь 610, согласно изложенному выше правилу, не нуждается в доработке.
Рассмотрим еще один пример, после чего сформулируем правило, которым особенно удобно пользоваться на первых порах, пока опыта в обращении дробей не так много. Так, дробь 1610000 после дописывания нулей в числителе будет иметь вид 001510000.
Как перевести обыкновенную дробь со знаменателем 10, 100, 1000 и т.д. в десятичную?
- Записываем и ставим после него запятую.
- Записываем число из числителя, которое получилось после дописывания нулей.
Теперь перейдем к примерам.
Переведем обыкновенную дробь в десятичную.
Сначала смотрим на дробь и видим, что никаких подготовительных действий проводить не нужно - количество цифр в числителе совпадает с количеством нулей в знаменателе.
Следуя правилу, записываем , ставим после него десятичную запятую и записываем число из числителя. Получаем десятичную дробь .
Разберем решение еще одного примера по этой теме.
Запишем дробь в виде десятичной дроби.
Количество нулей в знаменателе равно , а в числителе только три цифры. Допишем перед числом в числителе еще 4 нуля:
Теперь записываем , ставим после него десятичную запятую и записываем число из числителя. Получаем десятичную дробь .
Рассмотренные во всех примерах дроби - обыкновенные правильные дроби. Но как перевести неправильную обыкновенную дробь в десятичную? Сразу скажем, что необходимость в подготовке с дописыванием нулей для таких дробей отпадает. Сформулируем правило.
- Записываем число, которое находится в числителе.
- Десятичной запятой отделяем столько цифр справа, сколько нулей есть в знаменателе исходной обыкновенной дроби.
Ниже приведем пример на использование этого правила.
Переведем дробь из обыкновенной неправильной в десятичную.
Сначала запишем число из числителя:
Теперь справа отделим десятичной запятой пять цифр (количество нулей в знаменателе - пять). Получим:
Следующий вопрос, который закономерно возникает: как перевести в десятичную дробь смешанное число, если знаменателем его дробной части является число 10, 100, 1000 и т.д. Для обращения в десятичную дробь такого числа можно воспользоваться следующим правилом.
- Выполняем подготовку дробной части числа, если это необходимо.
- Записываем целую часть исходного числа и ставим после него запятую.
- Записываем число из числителя дробной части вместе с дописанными нулями.
Обратимся к примеру.
Переведем смешанное число в десятичную дробь.
В дробной части имеем выражение . Выполним его подготовку и допишем слева от числителя еще два нуля. Получим: .
Теперь записываем целую часть числа и ставим после него запятую:
После запятой записываем число из числителя вместе с нулями. Получаем результат:
Перевод обыкновенных дробей в конечные и бесконечные периодические дроби
Конечно, можно переводить в десятичные дроби и обыкновенные дроби со знаменателем, не равным 10, 100, 1000 и т.д.
Часто дробь можно легко привести к новому знаменателю, а затем уже воспользоваться правилом, изложенным в первом пункте данной статьи. Например, достаточно умножить числитель и знаменатель дроби 25 на 2, и мы получим дробь 410, которая легко приводится к десятичному виду 0,4.
Однако такой способ перевода обыкновенной дроби в десятичную удается использовать не всегда. Ниже рассмотрим, как поступать, если применить рассмотренный способ невозможно.
Принципиально новый способ обращения обыкновенной дроби в десятичную сводится к делению числителя на знаменатель столбиком. Эта операция очень похожа на деление натуральных чисел столбиком, но имеет свои особенности.
Числитель при делении представляется в виде десятичной дроби - справа от последней цифры числителя ставится запятая и дописываются нули. В получившемся частном десятичная запятая ставится тогда, когда заканчивается деление целой части числителя. Как именно работает этот способ, станет понятно после рассмотрения примеров.
Переведем обыкновенную дробь в десятичный вид.
Представим число из числителя в виде десятичной дроби, добавив после запятой несколько нулей.
Теперь разделим столбиком на . Первые три шага деления будут такими же, как при делении натуральных чисел, и мы получим.
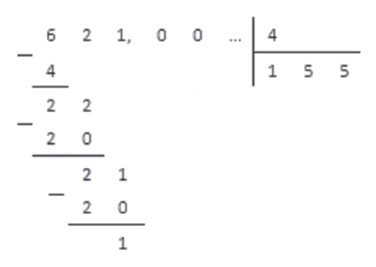
Когда мы добрались до десятичной запятой в делимом, а остаток отличен от нуля, ставим в частном десятичную запятую, и продолжаем делить, не обращая более внимания на запятую в делимом.
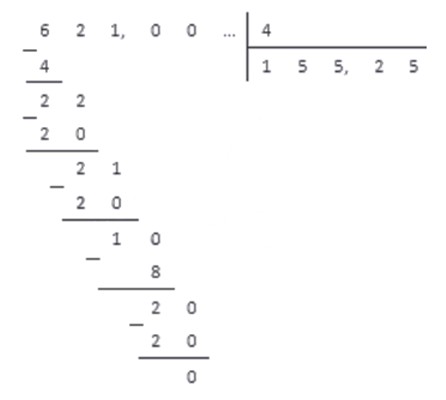
В итоге мы получаем десятичную дробь , которая и является результатом обращения обыкновенной дроби
Рассмотрим решение еще одного примера, чтобы закрепить материал.
Обратим обыкновенную дробь .
Для этого в столбик разделим дробь на . Деление целой части закончится на первом же шаге, поэтому сразу после него ставим в частном десятичную запятую и продолжаем деление, не обращая внимания на запятую в делимом до того момента, пока не получим остаток, равный нулю.
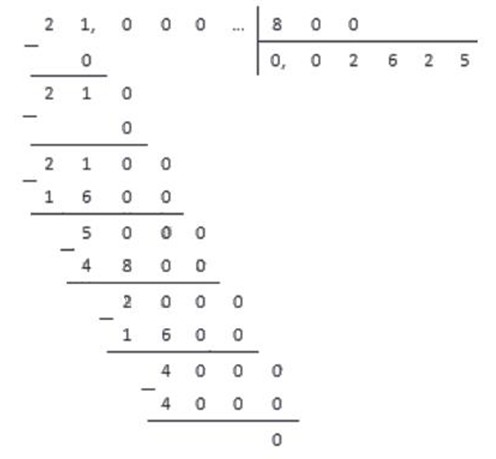
В результате мы получили: .
Но как быть, если при делении мы так и не получим в остатке 0. В таких случаях деление можно продолжать бесконечно долго. Однако, начиная с определенного шага, остатки будут периодически повторяться. Соответственно, будут повторяться и цифры в частном. Это значит, что обыкновенная дробь переводится в десятичную бесконечную периодическую дробь. Проиллюстрируем сказанное на примере.
Обратим обыкновенную дробь в десятичную. Для этого выполним деление столбиком.
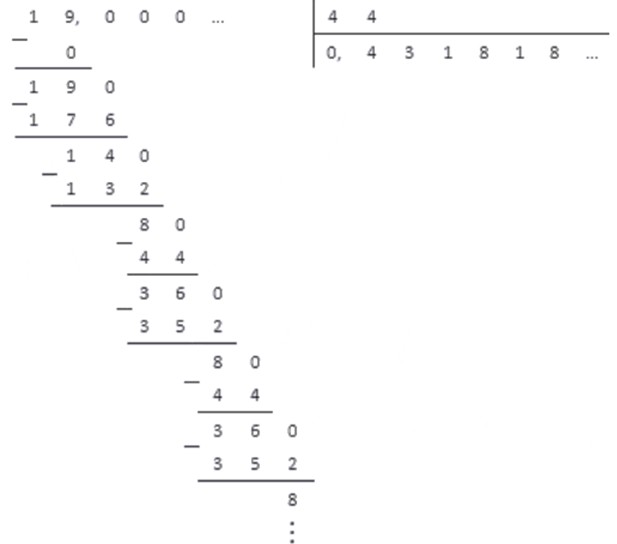
Мы видим, что при делении повторяются остатки и . При этом в частном повторяются цифры и . Это и есть период в десятичной дроби. При записи эти цифры берутся в скобки.
Таким образом, исходная обыкновенная дробь переведена в бесконечную периодическую десятичную дробь.
.
Пусть перед нами несократимая обыкновенная дробь. К какому виду она приведется? Какие обыкновенные дроби переводятся в конечные десятичные, а какие - в бесконечные периодические?
Во первых, скажем, что если дробь удается привести к одному из знаменателей 10, 100, 1000.., то она будет иметь вид конечной десятичной дроби. Чтобы дробь приводилась к одному из таких знаменателей, ее знаменатель должен быть делителем хотя бы одного из чисел 10, 100, 1000 и т.д. Из правил разложения чисел на простые множители следует, что делитель чисел 10, 100, 1000 и т.д. должен, при разложении на простые множители, содержать лишь числа 2 и 5.
Подытожим сказанное:
- Обыкновенную дробь можно привести к виду конечной десятичной дроби, если ее знаменатель можно разложить на простые множители 2 и 5.
- Если кроме чисел 2 и 5 в разложении знаменателя присутствуют другие простые числа, дробь приводится к виду бесконечной периодической десятичной дроби.
Приведем пример.
Какая из данных дробей переводится в конечную десятичную дробь, а какая - только в периодическую. Дадим ответ на этот вопрос, не выполняя непосредственно перевода обыкновенной дроби в десятичную.
Дробь , как легко заметить, умножением числителя и знаменателя на приводится к новому знаменателю .
. Отсюда делаем вывод, что данная дробь переводится в конечную десятичную дробь.
Разложение знаменателя дроби на множители дает . Так как простой множитель отличен от и от , данная дробь не может быть представлена в виде конечной десятичной дроби, а будет иметь вид бесконечной периодической дроби.
Дробь , во-первых, нужно сократить. После сокращения на получим несократимую дробь , разложение знаменателя которой на множители дает . Следовательно, это конечная десятичная дробь.
В случае с дробью разложение знаменателя на множители представляет собой само простое число . Соответственно, эту дробь можно обратить в бесконечную периодическую десятичную дробь.
Обыкновенную дробь нельзя перевести в бесконечную и непериодическую десятичную дробь
Выше мы говорили только о конечных и бесконечных периодических дробях. Но может ли какая-либо обыкновенная дробь быть обращена в вид бесконечной непериодической дроби?
Отвечаем: нет!
При переводе бесконечной дроби в десятичную получается либо конечная десятичная дробь, либо бесконечная периодическая десятичная дробь.
Остаток от деления всегда меньше делителя. Другими словами, согласно теореме о делимости, если мы делим какое-то натуральное число на число q, то остаток деления в любом случае не может быть больше, чем q-1. После окончания деления возможна одна из следующих ситуаций:
- Мы получаем в остатке 0, и на этом деление заканчивается.
- Мы получаем остаток, который при последующем делении повторяется, в результате мы имеем бесконечную периодическую дробь.
Иных вариантов при обращении обыкновенной дроби в десятичную не может быть. Скажем также, что длина периода (количество цифр) в бесконечной периодической дроби всегда меньше, чем число цифр в знаменателе соответствующей обыкновенной дроби.
Перевод десятичных дробей в обыкновенные дроби
Теперь пришло время рассмотреть обратный процесс перевода десятичной дроби в обыкновенную. Сформулируем правило перевода, которое включает три этапа. Как перевести десятичную дробь в обыкновенную?
- В числитель записываем число из исходной десятичной дроби, отбросив запятую и все нули слева, если они есть.
- В знаменатель записываем единицу и за ней столько нулей, сколько цифр есть в исходной десятичной дроби после запятой.
- При необходимости сокращаем полученную обыкновенную дробь.
Рассмотрим применение данного правила на примерах.
Представим число в виде обыкновенной дроби.
- В числитель записываем саму десятичную дробь, отбросив запятую: .
- В знаменателе пишем единицу, а после нее три нуля - именно столько цифр содержится в исходной дроби после запятой: .
- Полученную дробь можно сократить на , в результате чего мы получим: .
Переведем дробь из десятичных в обыкновенные.
- В числителе запишем дробь , отбросив запятую и нули слева. Получится .
- В знаменатель записываем единицу, а после нее пишем четыре нуля: . Данная дробь несократима.
Если в десятичной дроби есть целая часть, то такую дробь можно сразу перевести в смешанное число. Как это сделать?
Сформулируем еще одно правило.
- Число, стоящее в дроби до запятой, записываем как целая часть смешанного числа.
- В числителе записываем число, стоящее в дроби после запятой, отбросив нули слева, если они есть.
- В знаменателе дробной части дописываем единицу и столько нулей, сколько цифр есть в дробной части после запятой.
Обратимся к примеру
Представим дробь в виде смешанного числа.
- Записываем число , как целую часть.
- В числителе записываем цифры после запятой, отбросив нуль.
- В знаменателе записываем единицу и пять нулей
Поучаем смешанное число:
Дробную часть можно сократить на Сокращаем, и получаем финальный результат:
Перевод бесконечных периодических десятичных дробей в обыкновенные дроби
Разберем на примерах, как осуществлять перевод периодических десятичных дробей в обыкновенные. Прежде чем начать, уточним: любую периодическую десятичную дробь можно перевести в обыкновенную.
Самый простой случай - период дроби равен нулю. Периодическая дробь с нулевым периодом заменяется на конечную десятичную дробь, а процесс обращения такой дроби сводится к обращению конечной десятичной дроби.
Обратим периодическую дробь .
Отбросив нули справа, получим конечную десятичную дробь .
Обращая данную дробь в обыкновенную по алгоритму, разобранному в предыдущих пунктах, получаем:
.
Как быть, если период дроби отличен от нуля? Периодическую часть следует рассматривать как сумму членов геометрический прогрессии, которая убывает. Поясним это на примере:
Для суммы членов бесконечной убывающей геометрической прогрессии существует формула. Если первый член прогрессии равен , а знаменатель таков, что , то сумма равна .
Рассмотрим несколько примеров с применением данной формулы.
Пусть у нас есть периодическая дробь и нам нужно перевести ее в обыкновенную.
Запишем:
Здесь мы имеем бесконечную убывающую геометрическую прогрессию с первым членом и знаменателем .
Применим формулу:
Это и есть искомая обыкновенная дробь.
Для закрепления материала рассмотрим еще один пример.
Обратим дробь .
Сначала записываем дробь в виде бесконечной суммы:
Рассмотрим слагаемые в скобках. Эту геометрическую прогрессию можно представить в следующем виде:
.
Полученное прибавляем к конечной дроби и получаем результат:
После сложения данных дробей и сокращения получим окончательный ответ:
В завершение данной статьи скажем, что непериодические бесконечный десятичные дроби нельзя перевести в вид обыкновенных дробей.
