Сравнение целых чисел: правила, примеры

После того, как получили полное представление о целых числах, можно говорить об их сравнении.  Для этого выясняется, какие числа равные и неравные. Разберутся правила, благодаря которым выясняем, какие из двух неравных больше или меньше. Это правило основано на сравнении натуральных чисел. Будет рассмотрено сравнение трех и более целых чисел, нахождение наименьшего и наибольшего целого числа из заданного множества.

Равные и неравные целые числа

Сравнение двух чисел приводит к тому, что они либо равны либо не равны. Рассмотрим определения.

Отдельное место для обсуждения имеет $0$ и $-0$. Противоположное число $-0$ и есть $0$,  в этом случает эти два числа равнозначны.

Определение поможет сравнить заданные два числа. Возьмем, например, числа $-95$ и $-95$. Их запись полностью совпадает, то есть они считаются равными. Если взять числа $45$ и $-6897$, то визуально видно, что они отличаются и не считаются равными. Они имеют разные знаки.

Если числа равные, это записывается при помощи знака «$=$». Его расположение идет между числами. Если возьмем числа $-45$ и $-45$, то они равны. Запись принимает вид $-45=-45$. В случае, если числа неравны, тогда применяется знак «$\ne$». Рассмотрим на примере двух чисел: $57$ и $-69$. Эти числа целые, но не равные, так как запись отличается друг от друга.

При сравнивании чисел используется правило модуля числа.

Рассмотрим на примере данное определение.

Рассмотрим еще пример.

Если получаем неравные числа, тогда необходимо уточнение, какое из них меньше и какое больше.

Сравнение произвольных целых чисел с нулем

В предыдущем пункте было отмечено, что ноль равен сам себе даже со знаком минус. В таком случае равенства $0=0$ и $0=-0$ равнозначны и справедливы. При сравнении натуральных чисел имеем, что все натуральные числа больше нуля. Все целые положительные числа натуральные, поэтому и больше $0$.

При сравнении отрицательных чисел с нулем другая ситуация. Все числа, которые меньше нуля, считаются отрицательными. Отсюда делаем вывод, что любое отрицательное число меньше нуля, нуль равен нулю, а любое целое положительное больше нуля. Суть правила заключается в том, что нуль больше отрицательных чисел, но меньше всех положительных.

Например, числа $4, 57666, 677848$ больше, чем $0$, так как являются положительными. Отсюда следует, что нуль меньше указанных чисел, так как они со знаком $+$.

При сравнении отрицательных чисел дела обстоят иначе. Число $-1$ является целым и меньшим, чем $0$, так как имеет знак минус. Значит, $-50$ также меньше нуля. Но ноль больше всех  чисел со знаком минус.

Принимаются определенные обозначения для записи при помощи знаков меньше или больше, то есть $<$ и $>$. Такая запись, как $-24<0$ имеет значение, что $-24$ меньше нуля. Если необходимо записать, что одно число больше, чем другое, применяют знак $>$, например, $45>0$.

Сравнение положительных целых чисел

Рассмотрим еще один пример.

Сравнение целых отрицательных и положительных чисел

Сравним несколько чисел и рассмотрим на примере.

Сравнить заданные числа$-45$ и $23$. Видим, что $23$ – положительное число, а $45$ – отрицательное. Заметим, что $23$ больше $-45$

Если сравнивать $-1$ и $511$, то визуально понятно, что $-1$ меньше, так как имеет знак минус, а $511$ имеет знак $+$.

Сравнение целых отрицательных чисел

Рассмотрим правило сравнения:

Рассмотрим на примере.

Сравниваемые целые числа на координатной прямой

Рассмотрим целые числа, расположенные на координатной прямой.

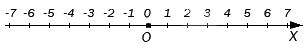
Из рассмотренных выше правил получим, что на горизонтальной координатной прямой точки, которым соответствуют большие целые числа, то есть лежат правее тех, которым соответствуют меньшие.

Из чисел $-1$ и $-6$ видно, что $-6$ лежит левее, а следовательно является меньше $-1$. Точка $2$ расположена правее $-7$, значит она больше.

Начало отсчета – это ноль. Он больше всех отрицательных и меньше всех положительных. Также и с точками, находящимися на координатной прямой.

Наибольшее отрицательное и наименьшее положительное целое число

В предыдущих пунктах подробно было рассмотрено сравнение двух целых чисел. В данном пункте поговорим о сравнении трех и более чисел, рассмотрим ситуации.

При сравнении трех и более чисел для начала составляются всевозможные пары. Например, рассмотрим для чисел $7, 17, 0$ и $-2$. Необходимо сравнить их попарно, то есть запись примет вид $7<17, 7>0, 7>-2, 17>0, 17>-2$ и $0>-2$. Результаты могут быть объединены в цепочку неравенств. Запись числе производится в порядке возрастания. В данном случае цепочка будет иметь вид $-2<0<7<17$.

Когда производится сравнение нескольких чисел, то появляется определение наибольшего и наименьшего значения числа.

Если множество состоит из 6 целых чисел, то запишем это так: $-4, -81, -4, 17, 0$ и $17$. Отсюда следует, что $-81<-4=-4<0<17=17$. Видно, что $-81$ – наименьшее число из данного множества, а $17$ – наибольшее. Это значит, что эти числа наибольшее и наименьшее только в заданном множестве.

Все числа множества необходимо записывать в порядке возрастания. Цепочка может быть бесконечной, как в данном случае: $\dots , -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, \dots$. Данный ряд запишется, как  $\dots <-5<-4<-3<-2<-1<0<1<2<3<4<5<\dots$ .

Очевидно, что множество целых чисел огромно и бесконечно, поэтому указать наименьшее или наибольшее число невозможно. Это можно сделать только в заданном множестве чисел. Число, расположенное правее на координатной прямой, всегда считается большим, чем то, которое левее.

Множество положительных чисел имеет наименьшее натуральное число, которое равно $1$. Ноль считается наименьшим неотрицательным числом.  Все числа, расположенные левее него отрицательные и меньше $0$.