- 16 июля 2025
- 7 минут
- 3 151
Сумма разрядных слагаемых натурального числа
Статью подготовили специалисты образовательного сервиса Zaochnik.
Представленная статья посвящена интересной теме о натуральных числах. Для того, чтобы выполнять некоторые действия, необходимо представлять исходные выражения как сложение нескольких чисел – другим языком, раскладывать числа по разрядам. Обратный процесс также очень важен для решения упражнений и задач.
В данном разделе детально рассмотрим типичные примеры для лучшего усвоения информации. Мы также научимся преобразовывать натуральные числа и записывать их в другом виде.
Каким образом можно разложить число по разрядам?
Исходя из названия статьи, можно сделать вывод, что этот параграф посвящен таким математическим терминам, как «сумма» и «слагаемые». Перед тем, как приступить к изучению данной информации, следует подробно изучить тему, чтобы иметь понятие о натуральных числах.
Приступим к работе и рассмотрим основные понятия о разрядных слагаемых.
Разрядные слагаемые – это определенные числа, которые состоят из нулей и единственной цифры, отличной от нуля. Натуральные числа относятся к данной категории, а числа – не относятся.
Количество разрядных слагаемых у представленного числа равняется тому числу, сколько цифр, отличных от нуля, содержится в записи. Если представить число как сумму разрядных слагаемых, так как и отличаются от . Если разложить число как сумму разрядных слагаемых, то оно представлено как сумма слагаемых. Три пятерки, представленные в записи, отличны от нуля.
Следует помнить, что все разрядные слагаемые числа содержат разное количество знаков в своей записи.
Сумма разрядных слагаемых натурального числа равна этому числу.
Перейдем к понятию разрядных слагаемых.
Разрядные слагаемые– это такие натуральные числа, в записи которых содержится цифра, отличная от нуля. Количество чисел должно быть равно количеству цифр, не равных нулю. Все слагаемые числа могут записываться с различным количеством знаков. Если мы раскладываем число по разрядам, то сумма слагаемых числа всегда будет равна этому числу.
Проанализировав понятие, можно сделать вывод, что однозначные и многозначные числа (полностью состоящие из нулей за исключением первой цифры) нельзя представить в качестве суммы. Это происходит потому, что данные числа сами будут разрядными слагаемыми для каких-то чисел. За исключением данных чисел, все остальные примеры могут раскладываться на слагаемые.
Как раскладывать числа?
Чтобы разложить число как сумму разрядных слагаемых, необходимо вспомнить, что натуральные числа связаны с количеством некоторых предметов. В записи числа разряды зависят от количества единиц, десятков, сотен, тысяч и так далее. Если вы возьмем, например, число , то может отметить, что он отвечает десяткам и единицам. Число соответствует сотне тысяч, десяткам тысяч, тысячам и сотням. Можно представить эти числа в виде равенств – и . В данных примерах мы наглядно увидели, как можно разложить число в виде разрядных слагаемых.
Смотря на этот пример, мы сможем любое натуральное число представить в виде суммы разрядных слагаемых.
Приведем еще один пример. Представим натуральное число в виде суммы разрядных слагаемых. Число соответствует десяткам и единицам, поэтому . А вот сумма не является суммой разрядных слагаемых числа , так как в ней не может быть двух чисел, состоящих из одинакового количества знаков.
Мы разобрали основные понятия. Разрядные слагаемые получили свое название из-за того, что каждое принадлежит к определенному разряду.
Как найти натуральное число, если известна сумма разрядных слагаемых?
Для того, чтобы разобрать данный пример, проанализируем обратную задачу. Представим, что нам известна сумма разрядных слагаемых. Нам необходимо найти данное натуральное число.
Например, сумма разложено по разрядам числа , а сумма соответствует натуральному числу . Таким образом, мы легко можем определить натуральное число, если нам известна его сумма резервных слагаемых.
Еще один способ нахождения натурального числа – это сложение в столбцах разрядных слагаемых. Данный пример не должен вызвать у вас сложности во время выполнения. Поговорим об этом подробнее.
Необходимо определить исходное число, если известна сумма разрядных слагаемых . Перейдем к решению. Необходимо записать числа и для сложения в столбик:

Осталось сложить числа по столбцам. Для этого нужно помнить, что сумма нулей равна нулю, а сумма нулей и натурального числа равна этому натуральному числу.
Получаем:
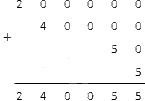
Выполнив сложение, мы получим натуральное число , сумма разрядных слагаемых которого имеет вид .
Поговорим еще об одном моменте. Если мы научимся раскладывать числа и представлять их в виде суммы разрядных слагаемых, то мы также сможем представлять натуральные число в виде суммы слагаемых, не являющихся разрядными.
Разложение по разрядам числа будет представлено как , а сумму разрядных слагаемых можно представить как или , или .
Иногда сложные вычисления можно немного упростить. Рассмотрим еще небольшой пример для закрепления информации.
Выполним вычитание чисел и . Для начала представим число в виде суммы разрядных слагаемых: . Выполнив действие, мы можем сделать вывод, что. сумме ( Тогда .
Математические онлайн-калькуляторы




