- 16 июля 2025
- 17 минут
- 3 180
Умножение натуральных чисел: правила, примеры, решения
Статью подготовили специалисты образовательного сервиса Zaochnik.
Имея общее представление об умножении натуральных чисел и их свойств, легче понять принцип выполнений действий над ними. Мы разберем правила, по которым производится умножение натуральных чисел. Весь материал имеет конкретные примеры и подробные объяснения. Совершим проверки результатов для того, чтобы сверить полученные на выходе числа.
Таблица умножения
Умножая два натуральных числа, получаем результат, который производится при умножении однозначных натуральных чисел. Произведение чисел и приравнивается к сумме, состоящей из трех слагаемых, равных числу . Иначе это запишем: . Таким же образом получены все результаты умноженных однозначных натуральных чисел. Все занесены в таблицу, приведенную ниже.
Это и есть таблица умножения. Все результаты сгруппированы для удобного дальнейшего применения. Таблица сложения натуральных чисел выглядит подобным образом. Она предоставлена ниже.
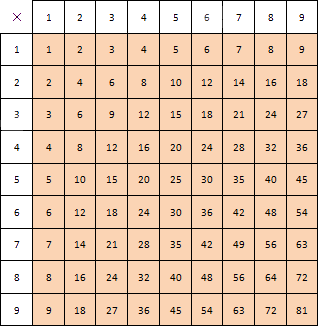
Чтобы выяснить, как пользоваться таблицей, приведем пример. Если необходимо найти произведение и , необходимо отметить столбец верхней ячейки, где имеем , и строку левой ячейки, где число . Чтобы найти результат, следует найти их общую ячейку, то есть пересечение столбца и строки. На рисунке ниже изображен пример нахождения искомого умножения и .
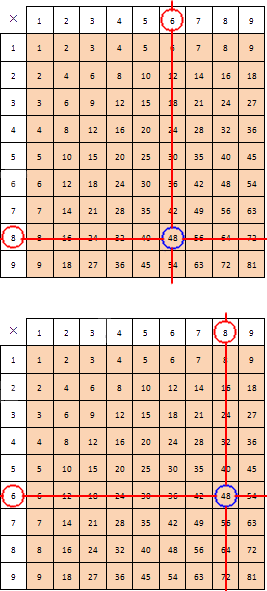
Умножение трех и более количества чисел
Мы дали определение понятию умножения двух чисел. Теперь поговорим об умножении трех и более имеющихся чисел. Таким образом, в такой ситуации применимо сочетательное свойство умножения натуральных чисел.
Сочетательное свойство умножения показывает равнозначность двух произведений и , где и могут быть любыми числами. Результат умножения данных чисел не будет зависеть от местоположения скобок. Поэтому чаще всего при произведении скобки отсутствуют, а запись имеет вид . Данное выражение называют произведением трех чисел, причем все входящие в него числа – множители.
Сочетательное свойство умножения необходимо для того, чтобы легче было выявлять равные произведения. Это значит, что из приведенных и можно сделать вывод, что они все равные. Положение скобок при умножении не играет роли. Это произведение может быть записано в виде .
Обычно скобки опускаются при умножении. Произведение нескольких трех и более чисел без скобок приводит к последовательной замене двух соседних множителей до получения необходимого результата. Скобки могут быть расставлены произвольно, так как итог произведения не изменится.
Если взять пять натуральных чисел и записать их в виде произведения, то получим . Имеется два основных способы решения.
Первый способ заключается в том, что два множителя слева будут последовательно заменяться произведением. Тогда получим, что . Так как , то . Далее имеем, что , тогда в итоге получим результат . Умножение пяти заданных чисел будет равняться . Этот способ записывается, как .
Второй способ заключается в том, что скобки располагаются таким образом . Имеем, что и , то . При равном получим, что . В итоге получим, что . Отсюда следует, что .
Порядок следования множителей не влияет на результат. Множители могут быть записаны в любом порядке. Это следует из свойств умножения натуральных чисел.
Даны четыре числа для умножения: . Их произведение записывается в виде .
При замене произведения множителей и или и получим, что следующий этап необходимо будет произвести умножение двузначных чисел и .
Чтобы избежать это, необходимо поменять слагаемые местами, иначе расставить скобки.
Тогда получим:.
При перемене мест множителей можно производить наиболее удобные комбинирования для вычисления. Рассмотрим задание, где решение приводит к умножению нескольких чисел.
Каждая коробка имеет по предмета. В ящики положили коробки. Какое количество предметов будет в ящиках?
Решение
Нам дано, что в одном ящике коробки, а в них соответственно по предмета.
Тогда в одном ящике предметов. Отсюда получим, что в ящиках предмета. Можно рассуждать иным образом. Один ящик вмещает в себя коробки, отсюда в ящиках коробок. Каждая из коробок имеет предмета, тогда имеем, что коробок содержат предмета.
Эти решения можно записать таким образом или .
Делаем вывод, что искомое количество предметов – это произведение , а значит, что .
Ответ: .
Подведем итоги.
При умножении трех и более чисел действия производятся последовательно. Используя переместительное и сочетательное свойства умножения, разрешается менять местами множителями и заменять их двумя другими умножаемыми числами.
Умножение суммы на натуральное число и наоборот
Благодаря распределительному свойству умножения сложение и умножение связаны. Это помогает в изучении сложения и умножения. Свойство способствует углубиться в изучение всех действий.
Если рассматривать распределительное свойство умножения относительно сложения, то получим такой вид записи с двумя слагаемыми: , где являются произвольными натуральными числами. Исходя из данного равенства при помощи метода математической индукции докажем справедливость предложенного и т.д., где являются натуральными числами.
Отсюда следует, что произведение суммы нескольких чисел и данного числа равна сумме произведений каждого из слагаемых с данным числом. Это правило применимо при умножении на заданное число.
Если взять сумму из пяти чисел на , получим, что . Отсюда имеем, что то , после чего находим сумму чисел .
Можно было сделать вычисления иначе, тогда следовало посчитать сумму, после чего умножение. Этот случай менее удобен, так как умножение двухзначного числа на мы пока не выполняли. Умножение двухзначных чисел – это тема, показанная в разделе умножения многозначного и однозначного натуральных чисел.
Используя переместительное свойство, мы можем переформулировать правило умножения суммы чисел на заданное число таким образом: произведение данного числа и суммы нескольких чисел равняется сумме произведений данного числа и каждого из слагаемых. Это правило умножения данного числа на заданную сумму.
Например, . Здесь применяем правила умножения числа на сумму.
Рассмотрим конкретный пример, где умножение решение сводится к умножению суммы чисел на данное число.
В коробке находятся по красных, зеленых и синих предмета. Какой количество предметов имеется во всех четырех коробках?
Решение
Для определения количества предметов в одной коробке, вычислим . Отсюда следует, что четыре коробки содержат в раза больше, значит, предметов.
Находим произведение суммы на число, применив полученное правило, тогда .
Ответ: предметов.
Умножение натурального числа на 10, 100, 1000 и так далее
Чтобы получить правило произвольного умножения натурального числа на , рассмотрим подробно.
Натуральные числа вида соответствуют десяткам. Это значит, что отсюда следует, что умножением двух натуральных чисел их смысл суммы должен быть идентичным, тогда получим .
Таким же образом можно прийти к следующим неравенствам:
Выходит, что десяток десятков – это сотня, то ;
что десяток сотен – это тысяча, тогда ;
что десяток тысяч – это десять тысяч, то .
Исходя из рассуждений, получим
рассмотрим пример для формулировки правила умножения произвольного натурального числа на 10.
Необходимо произвести умножение натурального числа на .
Решение
Чтобы быстрее подсчитать, необходимо представить число в виде суммы разрядных слагаемых.
Применим правило умножения суммы на число из предыдущего пункта, тогда получим . Число можно представить в виде произведения , число произведением .
Отсюда получим, что сумма будет равна сумме . Тогда сочетательное свойство умножения можно зафиксировать, как .
Отсюда получим, что . Сумма, полученная в результате, представляет собой разложение по рядам числа .
Ответ: .
Аналогичным способом мы можем умножить любое натуральное число на . В таких случаях запись всегда будет оканчиваться на .
Приведенные примеры и рассуждения дают возможность перейти к правилу умножения произвольного натурального число на . Если в конце записи дописать цифру , тогда заданное число будет служить результатом умножения на . Когда в записи натурального числа дописывают , то полученное число применяется как результат умножения на .
Приведем примеры: и так далее.
Основываясь на правиле умножения натурального числа на , можно получить умножение произвольного числа на и выше.
Если ,тогда умножение натурального числа на приводит к умножению числа на и еще одному умножению на .
Тогда получим:
.
Если полученная запись имеет на цифры больше, тогда считается, что это результат умножения всего числа на . Это и называется правилом умножения числа на .
Произведение , тогда умножение любого натурального числа на приводит к умножению заданного числа на и еще одному умножению на . Отсюда следует, что это правило умножения произвольного натурального числа на . Когда в записи имеется цифры , тогда считают, что это результат умножения числа на .
Таким же образом производится умножение на и так далее. Идет дописывание нулей в конце числа.
В качестве примера запишем:
Умножение многозначного и однозначного натуральных чисел
Имея навыки для выполнения умножения, разберем все правила на примере.
Найти произведение трехзначного числа на .
Решение
Для начала представляем число в виде суммы разрядных слагаемых. Здесь получим, что . Отсюда получим, что .
Используя правило умножения суммы на число, получим, что:
.
Произведения и и сумма записывается, как .
Применив переместительное и сочетательное свойство, получим .
Так как и , то .
Выполняем умножение на , на . После этого выполняем сложение
Ответ: произведение и .
Чтобы закрепить материал, необходимо рассмотреть пример умножения.
Найти произведение и .
Решение
Ответ: результат умножения и .
Умножение двух многозначных натуральных чисел
Умножение двух многозначных натуральных чисел производится таким образом, что один из множителей раскладывается по разрядам, после этого применяют правило умножения на сумму. Изучение предыдущих статей позволит быстрее разобраться с имеющимся разделом.
Вычислить произведение и .
Решение
Необходимо произвести разложение числа по разрядам , тогда .
Правило умножения применимо для .
Так как и , тогда справедливо равенство .
Сочетательное свойство способствует записи последней суммы .
Вычисляя произведения и , представляем его в виде суммы
Получим, что
Вычислим сумму натуральных чисел:
Ответ: Произведение и .
Теперь умеем умножать два любых натуральных числа.
Проверка результата умножения натуральных чисел
Умножение всегда требует проверки. Она производится при помощи деления по правилу: полученное произведение делят на один из множителей. Если полученное число равно одному из множителей, тогда вычисление произведено правильно. Если нет, то допущена ошибка.
Произвести умножение на , равное . Необходимо выполнить проверку.
Решение
Проверка производится посредством деления на . Тогда получим, что .
Если получим число, равное одному из множителей, тогда задание решено верно.
Произведено умножение на . Результат равен . Выполнить проверку.
Решение
Для выполнения проверки необходимо разделить на . Должны получить число . Производится делением столбиком:
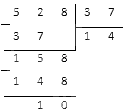
При делении мы выявили, что делится на , но с остатком. Отсюда следует, что умножение на было выполнено неверно.
Ответ: проверка показала, что умножение было выполнено неверно.
Вычислить произведение чисел и , после чего выполнить проверку.
Решение
Представляем число в виде суммы . Применим свойство умножения суммы двух чисел на натуральное число. Получим, что .
Для выполнения проверки, разделим на . Значит, умножение произведено верно.
Ответ: .
Математические онлайн-калькуляторы




