- 16 июля 2025
- 4 минуты
- 3 948
Умножение отрицательных чисел: правило, примеры
Статью подготовили специалисты образовательного сервиса Zaochnik.
В данной статье сформулируем правило умножения отрицательных чисел и дадим ему объяснение. Будет подробно рассмотрен процесс умножения отрицательных чисел. На примерах показаны все возможные случаи.
Умножение отрицательных чисел
Правило умножения отрицательных чисел заключается в том, что для того, чтобы умножить два отрицательных числа, необходимо перемножить их модули. Данное правило записывается так: для любых отрицательных чисел данное равенство считается верным.
Выше приведено правило умножения двух отрицательных чисел. Исходя из него, докажем выражение: . Статья умножение чисел с разными знаками рассказывает о том, что равенств справедливое, как и . Это следует из свойства противоположных чисел, благодаря которому равенства запишутся следующим образом:
.
Тут явно видно доказательство правила умножения отрицательных чисел. Исходя из примеров явно, что произведение двух отрицательных чисел – положительное число. При перемножении модулей чисел результат всегда положительное число.
Данное правило применимо для умножения действительных чисел, рациональных чисел, целых чисел.
Примеры умножения отрицательных чисел
Теперь рассмотрим подробно примеры умножения двух отрицательных чисел. При вычислении необходимо пользоваться правилом, написанным выше.
Произвести умножение чисел и .
Решение.
По модулю умножаемые данные два числа равны положительным числам и . Их произведение дает в результате . Отсюда следует, что произведение заданных чисел равно
Запишем кратко само умножение отрицательных чисел:
Ответ: .
При умножении отрицательных рациональных чисел, применив разобранное правило, можно мобилизоваться к умножению дробей, умножению смешанных чисел, умножению десятичных дробей.
Вычислить произведение .
Решение.
Используя правило умножения отрицательных чисел, получим, что . Для получения результата необходимо выполнить умножение десятичной дроби на натуральное число столбиков. Это выглядит так:
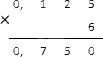
Получили, что выражение примет вид .
Ответ: .
В случае, когда множители – иррациональные числа, тогда их произведение может быть записано в виде числового выражения. Значение вычисляется только по необходимости.
Необходимо произвести умножение отрицательного на неотрицательное .
Решение
Находим модули заданных чисел:
и .
Следуя из правил умножения отрицательных чисел, получим результат . Это выражение и является ответом.
Ответ: .
Для продолжения изучения темы необходимо повторить раздел умножение действительных чисел.
Математические онлайн-калькуляторы




